LCM, GCD, and MOD

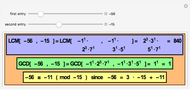
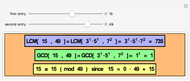
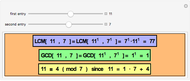
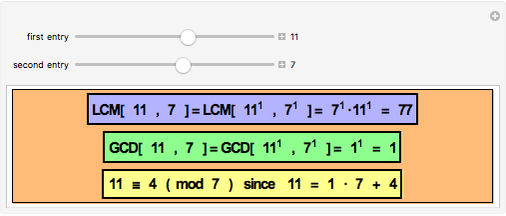
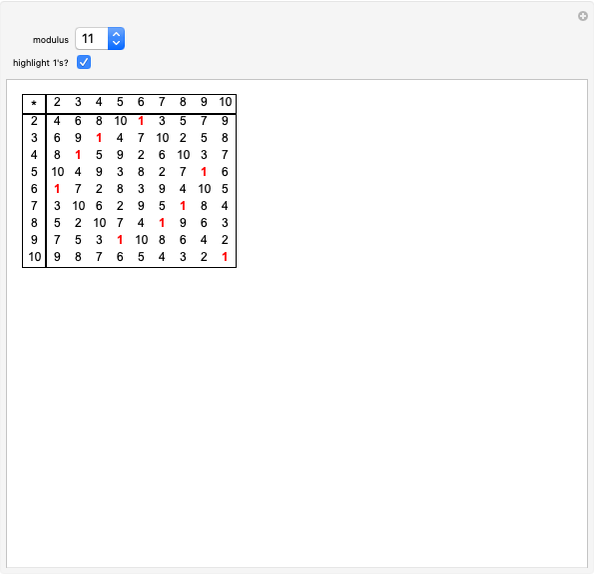
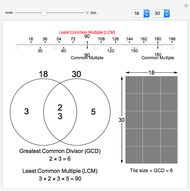
This Demonstration illustrates the concepts of the least common multiple (LCM) and the greatest common divisor (GCD). It depends on explicit factoring; the factorization is used to show the GCD and LCM. The Euclidean algorithm finds the GCD much more efficiently because it does not rely on factoring. In any case, you can find the LCM of and from the GCD: .

You can also see how to perform some basic modular arithmetic.