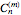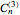Labeled Fuss-Catalan Polygon Divisions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
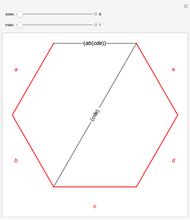
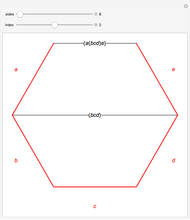
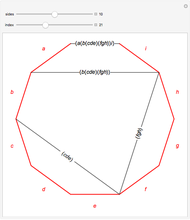
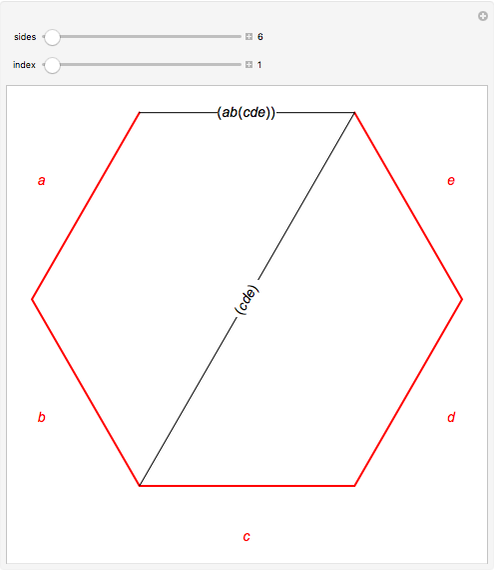
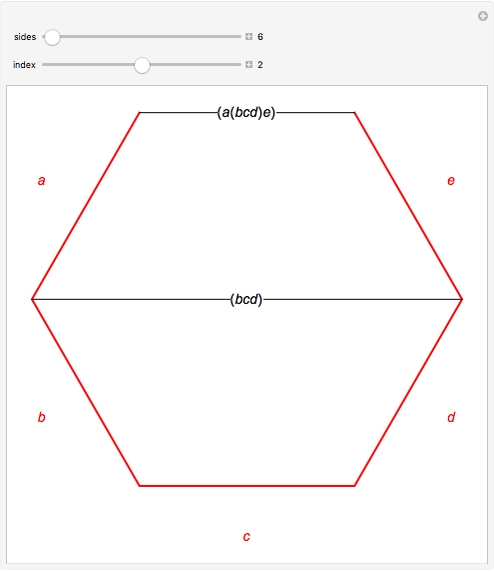
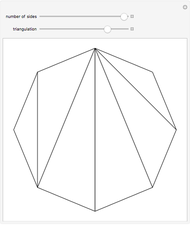
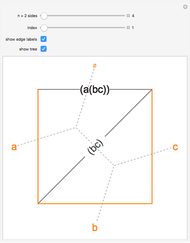
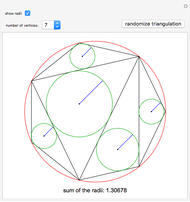
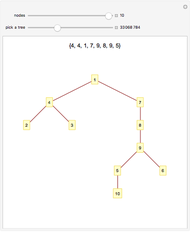
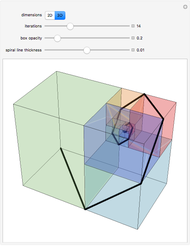
The Catalan numbers  have many interpretations in combinatorics, two of them being the number of ways to insert parentheses into a sequence of numbers so that they are grouped into pairs—for example, ((12)3) and (1(23))—and the number of ways to divide a polygon into triangles.
have many interpretations in combinatorics, two of them being the number of ways to insert parentheses into a sequence of numbers so that they are grouped into pairs—for example, ((12)3) and (1(23))—and the number of ways to divide a polygon into triangles.
Contributed by: Robert Dickau (February 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] R. P. Stanley, Enumerative Combinatorics, Vol. 2, New York: Cambridge University Press, 1999 pp. 212, 234 (Exercise 6.33(c)).
[2] R. L. Graham, D. E. Knuth and O. Patashnik, Concrete Mathematics: A Foundation for Computer Science, 2nd ed., Reading, MA: Addison-Wesley, 1994 p. 361.
[3] M. Gardner, Time Travel and Other Mathematical Bewilderments, New York: W. H. Freeman, 1988 Chapter 20.
Permanent Citation