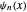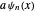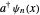Ladder Operators for the Harmonic Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
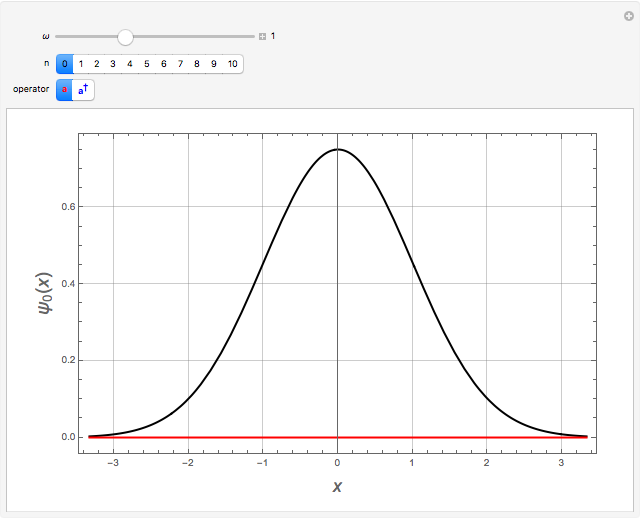
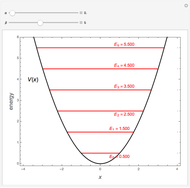
The Hamiltonian for the linear harmonic oscillator can be written 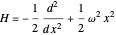 , in units with
, in units with 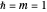 . The eigenstates are given by
. The eigenstates are given by 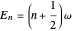 ,
, 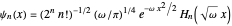 ,
, 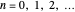 , where
, where 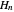 is a Hermite polynomial. An alternative reformulation of the problem can be based on the representation
is a Hermite polynomial. An alternative reformulation of the problem can be based on the representation  in terms of ladder operators
in terms of ladder operators 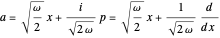 and
and 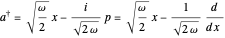 . The step-down or annihilation operator
. The step-down or annihilation operator 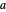 acts on the eigenfunctions according to
acts on the eigenfunctions according to 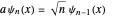 , with
, with  . The step-up or creation operator
. The step-up or creation operator 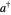 satisfies
satisfies 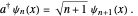
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
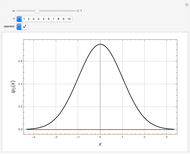
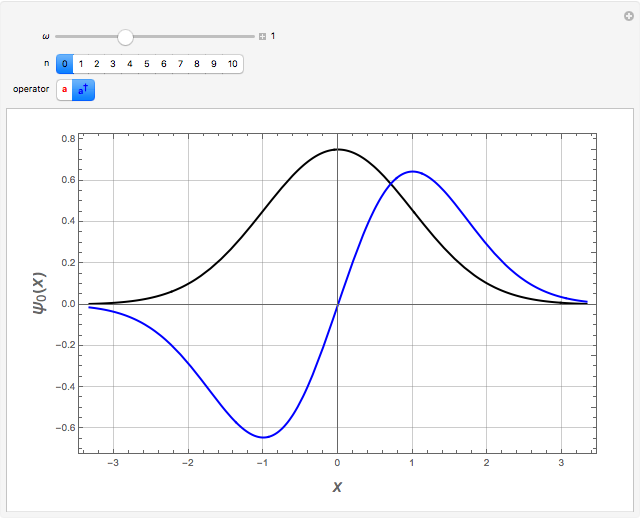
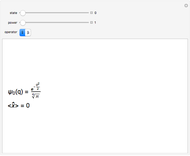
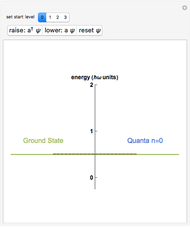
Snapshot 1: 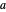 annihilates the ground state:
annihilates the ground state: 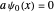
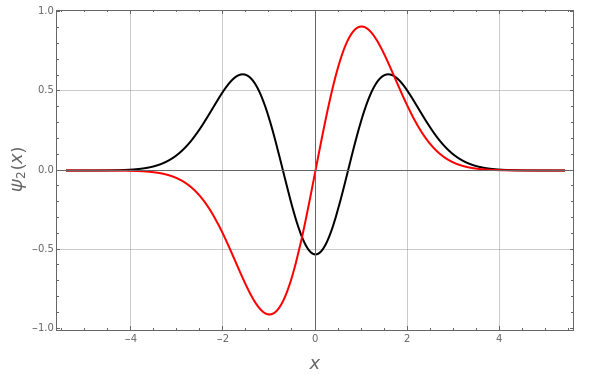
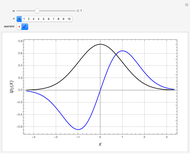
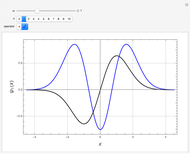
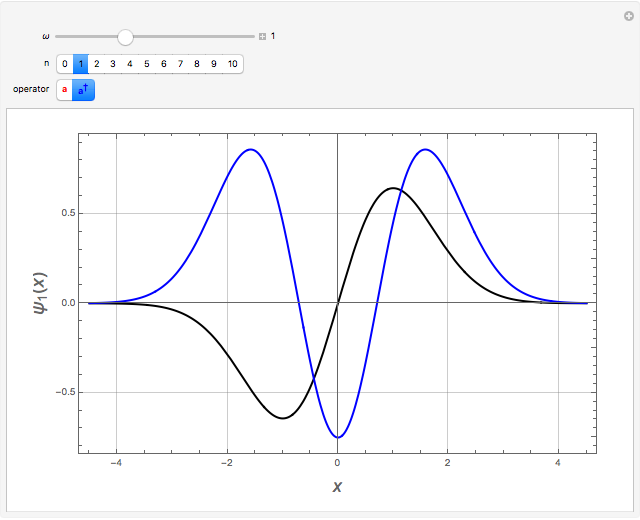
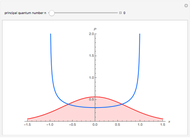
Snapshots 2 and 3: 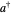 raises the states
raises the states  and
and 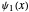 by one level
by one level
Reference: S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, 2004 pp. 66–68.
Permanent Citation