Laminar Flow of a Power-Law Fluid in a Horizontal Pipe

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
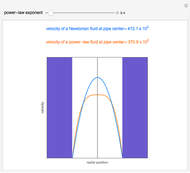
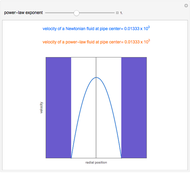
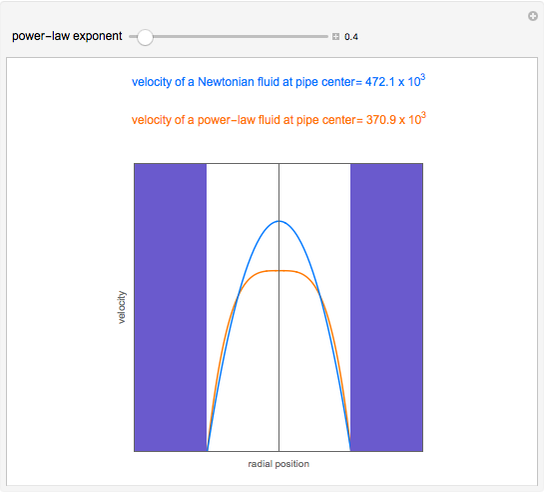
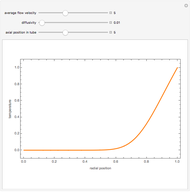
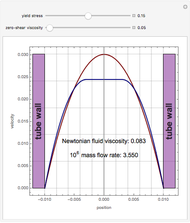
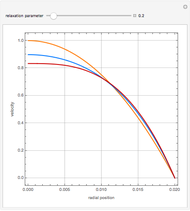
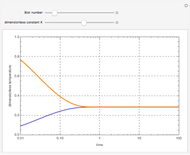
The velocity profile versus radial position is obtained for the laminar flow of a pseudo-plastic or dilatant fluid (orange curve) and a Newtonian fluid (blue curve) in a pipe under the assumption of equal volumetric flow rate. The pipe radius is 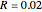 and the applied pressure gradient is
and the applied pressure gradient is 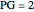 . The power-law consistency index is chosen to be
. The power-law consistency index is chosen to be 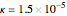 . If the power-law exponent
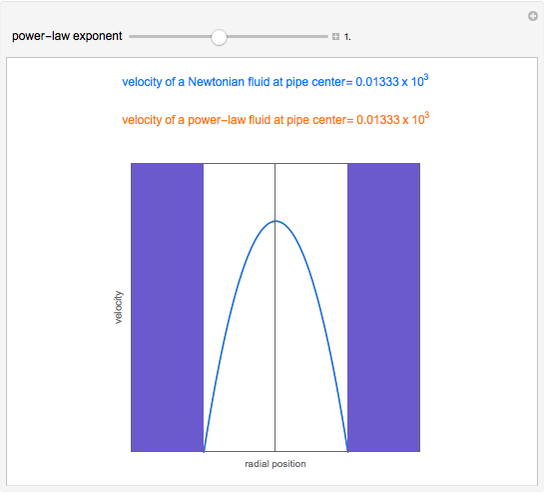
. If the power-law exponent  is 1, then a Newtonian fluid is recovered. For the pseudo-plastic fluid, the velocity profile is flatter near the center, where it resembles plug flow, and is steeper near the wall, where it has a higher velocity than the Newtonian fluid or the dilatant fluid. Thus, convective energy transport is higher for shear-thinning fluids when compared to shear-thickening or Newtonian fluids.
is 1, then a Newtonian fluid is recovered. For the pseudo-plastic fluid, the velocity profile is flatter near the center, where it resembles plug flow, and is steeper near the wall, where it has a higher velocity than the Newtonian fluid or the dilatant fluid. Thus, convective energy transport is higher for shear-thinning fluids when compared to shear-thickening or Newtonian fluids.
Contributed by: Housam Binous (June 2008)
Open content licensed under CC BY-NC-SA
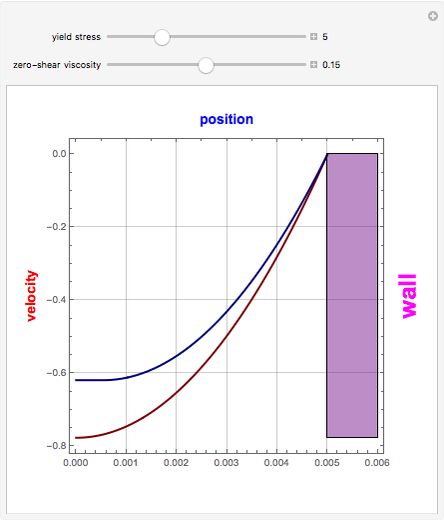
Snapshots
Details
A non-Newtonian fluid has a viscosity that changes with the applied shear force. For a Newtonian fluid (such as water), the viscosity is independent of how fast it is stirred, but for a non-Newtonian fluid the viscosity is dependent. It gets easier or harder to stir faster for different types of non-Newtonian fluids. Different constitutive equations, giving rise to various models of non-Newtonian fluids, have been proposed in order to express the viscosity as a function of the strain rate. In power-law fluids, the following relation is satisfied: 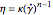 , where
, where  is the power-law exponent and
is the power-law exponent and  is the power-law consistency index. Dilatant or shear-thickening fluids correspond to the case where the exponent in this equation is positive, while pseudo-plastic or shear-thinning fluids are obtained when
is the power-law consistency index. Dilatant or shear-thickening fluids correspond to the case where the exponent in this equation is positive, while pseudo-plastic or shear-thinning fluids are obtained when 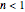 . The viscosity decreases with strain rate for
. The viscosity decreases with strain rate for 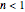 , which is the case for pseudo-plastic fluids (also called shear-thinning fluids). On the other hand, dilatant fluids are shear-thickening. If
, which is the case for pseudo-plastic fluids (also called shear-thinning fluids). On the other hand, dilatant fluids are shear-thickening. If  , the Newtonian fluid behavior can be recovered.
, the Newtonian fluid behavior can be recovered.
Permanent Citation