Langmuir Isotherms for a Binary Mixture

Initializing live version

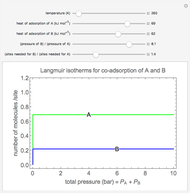
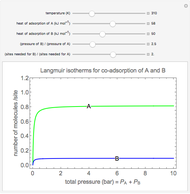
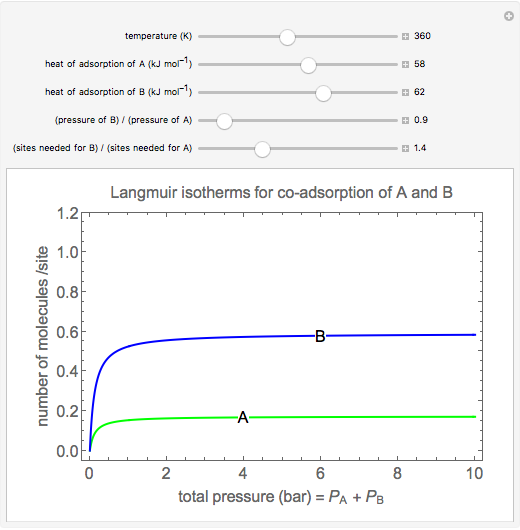
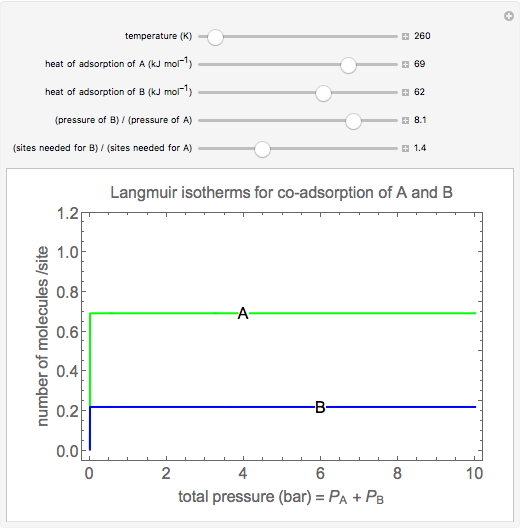
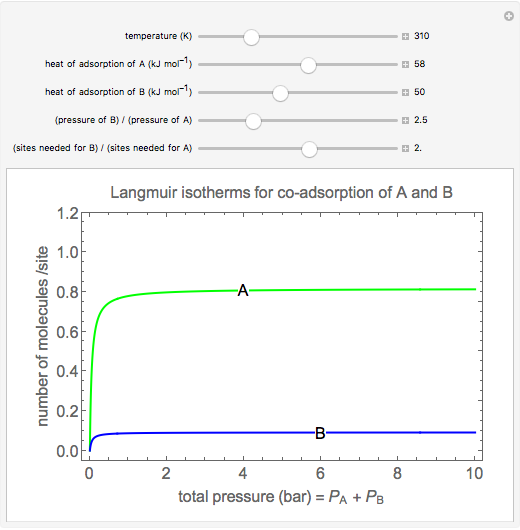
Langmuir isotherms are generated for each component in a binary gas-phase mixture of and . Vary the heats of adsorption of each component, the temperature, and the ratio of partial pressures with sliders. The molecules compete for adsorption sites but do not interact with each other, and this is taken into account in the form of the Langmuir isotherm. Vary the relative number of sites per molecule with a slider to account for larger molecules occupying more surface area than smaller molecules. The Langmuir isotherm for molecules and has the form:

[more]

Contributed by: Rachael L. Baumann (February 2014)
Additional contributions by: John L. Falconer and Nick Bongiardina
(University of Colorado, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The number of molecules per site for components and are:

where is the adsorption equilibrium constant for component (1/bar), is the partial pressure (bar), and is the saturation coverage of to .

where is a pre-exponential factor (1/bar), is the heat of adsorption (kJ/mol), is the ideal gas constant (kJ/[mol K]), and is temperature (K).

where 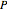is the total pressure (bar), and is the ratio of partial pressures.

The screencast video at [1] shows how to use this Demonstration.

Reference

[1] Langmuir Isotherms for a Binary Mixture. www.colorado.edu/learncheme/kinetics/LanmuirIsothermsBinaryMixture.html.

Permanent Citation

Rachael L. Baumann "Langmuir Isotherms for a Binary Mixture"
http://demonstrations.wolfram.com/LangmuirIsothermsForABinaryMixture/
Wolfram Demonstrations Project
Published: February 26 2014


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send

Langmuir Isotherms for a Binary Mixture

Snapshots

Details

Related Links

Permanent Citation