Lens Aberrations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
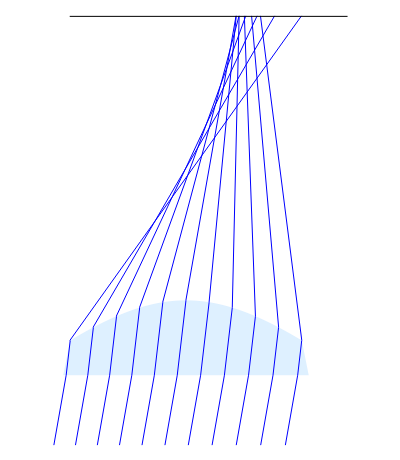
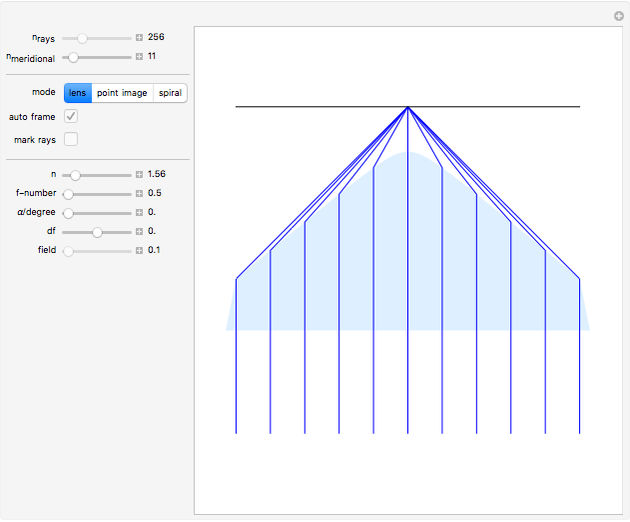
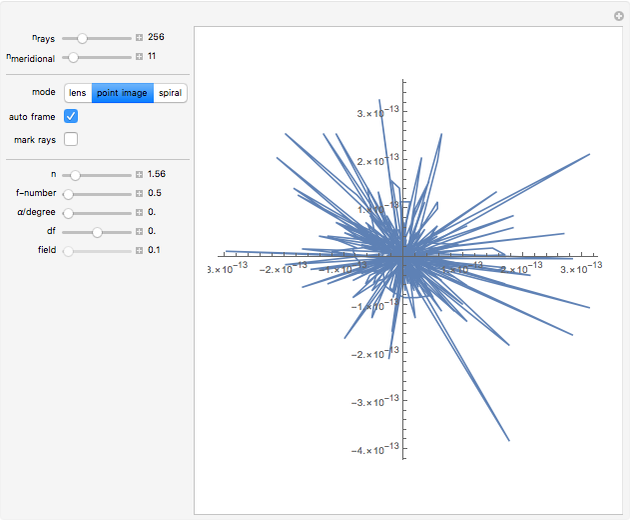
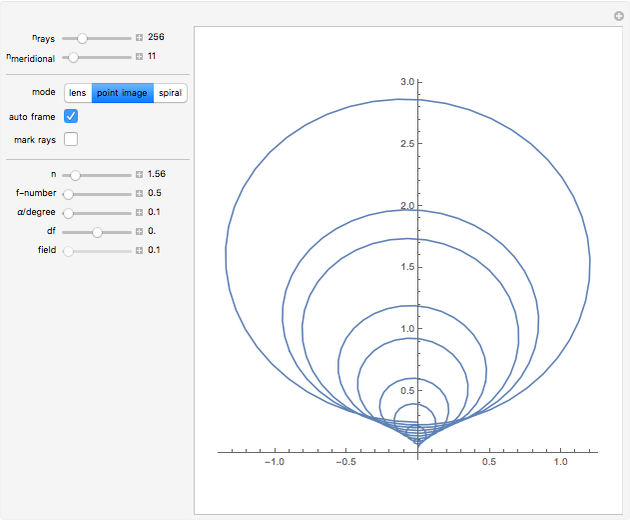
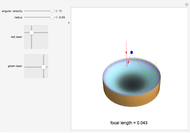
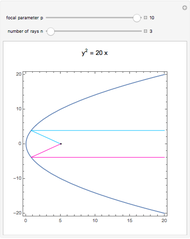
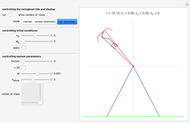
This Demonstration shows how a plano-convex lens acts on a bundle of parallel light rays. Ideally, a collecting lens would deflect all these rays to meet at a single point. If the rays are parallel to the optical axis, this can indeed be achieved by a convex lens surface in the form of a rotating hyperbola, which was already known to Descartes, Huygens, and Newton. For parallel bundles that form a small angle with the optical axis, the concentration to a point holds only approximately. When deflected into an extended light spot, the oblique rays form surprisingly complex and beautiful patterns that can be studied by mode set to "point image".
[more]
Contributed by: Ulrich Mutze (January 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
By setting the inclination angle  different from zero we see that the ideal focusing property gets lost rapidly with increasing
different from zero we see that the ideal focusing property gets lost rapidly with increasing  . As a consequence, the imaging capability even for small objects in the center of the field of view is not significantly better than that of a plano-convex lens with a spherical surface. This was not known when the unique focusing property of hyperbolic lenses was discovered. This discovery and the enthusiasm it created is brilliantly described in [1]: Aristotle already posed the problem of a perfectly focusing curve, "the anaclastic", for which a hyperbola is a solution. Kepler was the first to find this solution, although without a correct proof. Descartes was the first to give a valid proof that a plano-convex hyperbolic lens (with geometric data matching the refractive index in a manner derived by him) has the property of focusing axis-parallel rays exactly in one point. Descartes held the opinion that a telescope with such a hyperbolic objective lens would show "whether there are animals on the moon". He did not foresee the limitations caused by light dispersion and diffraction. The destructive effect of the former—the colored fringes from chromatic aberration—were known to Descartes. He thought, however, that they originate from imperfections of the manual lens grinding process and hoped to get rid of these by ingenious mechanical grinding machines that he designed. He spent much time and energy finding craftsmen willing and capable of building such machines. He thought that using machines would be the only way to make a hyperbolic surface profile with sufficient accuracy. In modern optics, hyperbolic lens surfaces are only one species among many kinds of aspherical surfaces that are omnipresent in all but the most simple photographic lenses.
. As a consequence, the imaging capability even for small objects in the center of the field of view is not significantly better than that of a plano-convex lens with a spherical surface. This was not known when the unique focusing property of hyperbolic lenses was discovered. This discovery and the enthusiasm it created is brilliantly described in [1]: Aristotle already posed the problem of a perfectly focusing curve, "the anaclastic", for which a hyperbola is a solution. Kepler was the first to find this solution, although without a correct proof. Descartes was the first to give a valid proof that a plano-convex hyperbolic lens (with geometric data matching the refractive index in a manner derived by him) has the property of focusing axis-parallel rays exactly in one point. Descartes held the opinion that a telescope with such a hyperbolic objective lens would show "whether there are animals on the moon". He did not foresee the limitations caused by light dispersion and diffraction. The destructive effect of the former—the colored fringes from chromatic aberration—were known to Descartes. He thought, however, that they originate from imperfections of the manual lens grinding process and hoped to get rid of these by ingenious mechanical grinding machines that he designed. He spent much time and energy finding craftsmen willing and capable of building such machines. He thought that using machines would be the only way to make a hyperbolic surface profile with sufficient accuracy. In modern optics, hyperbolic lens surfaces are only one species among many kinds of aspherical surfaces that are omnipresent in all but the most simple photographic lenses.
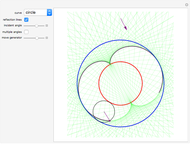
Snapshot 1: a hyperbolic lens in which the hyperbola is close to its asymptotes
Snapshot 2: on axis, where the computed rays intersect the image plane; the deviation from perfect focusing is due to numerical noise
Snapshot 3: only 0.1 degrees off-axis: the computed rays form an extended light spot dominated by a coma
Snapshot 4: 0.3 degrees off axis and 4% out of focus: astigmatism becomes noticeable
Snapshot 5: where the computed rays intersect the hyperbolic lens surface
Reference
[1] D. G. Burnett, Descartes and the Hyperbolic Quest: Lens Making Machines and Their Significance in the Seventeenth Century, Philadelphia: American Philosophical Society, 2005.
Permanent Citation