Level Surfaces for a Polynomial

Initializing live version

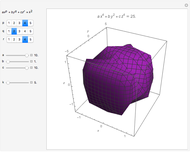
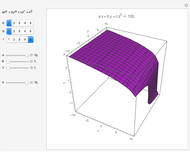
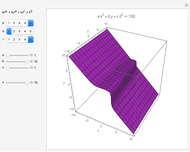
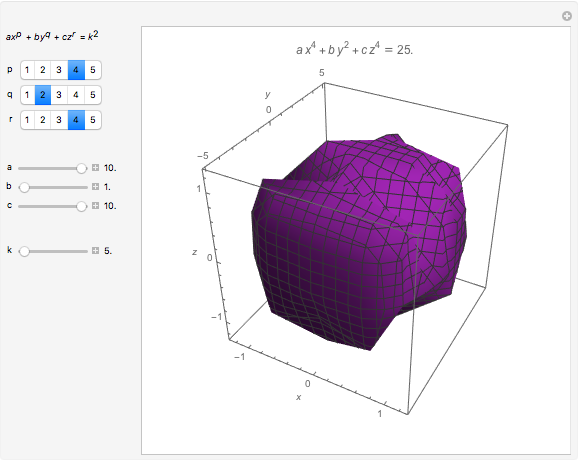
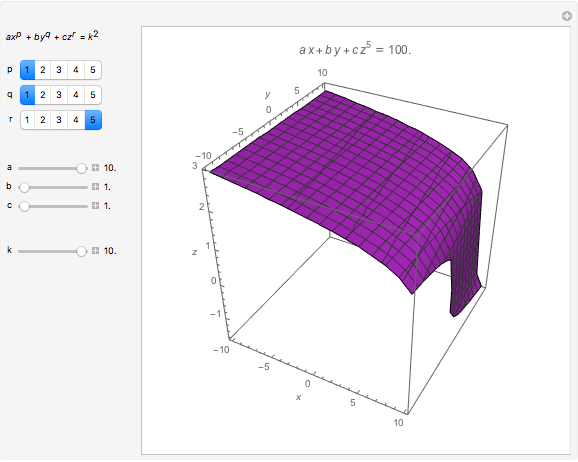
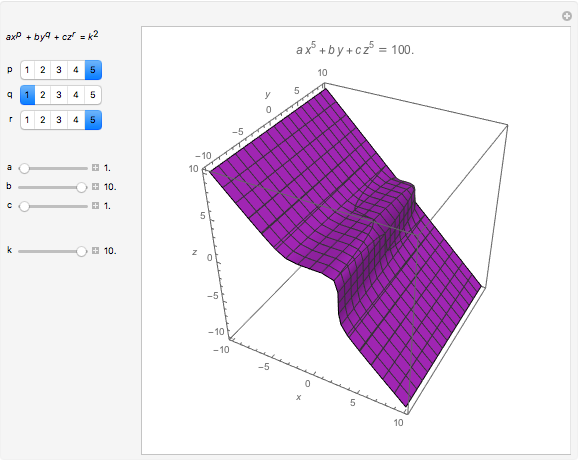
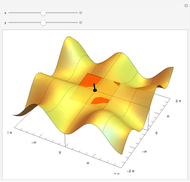
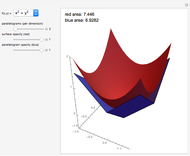
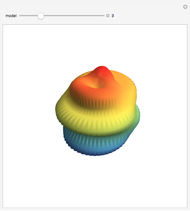
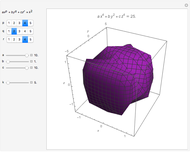
Let 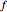be a function of three variables and let be a constant. The set of all points 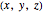in space such that 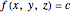is called a level surface of 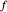(with value ).

Contributed by: Osman Tuna Gökgöz (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Reference:

J. Marsden and A. Weinstein, Calculus III, New York: Springer, 1985 p. 713.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send