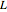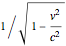Light Clocks and Time Dilation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
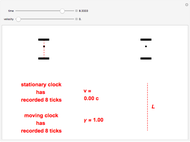
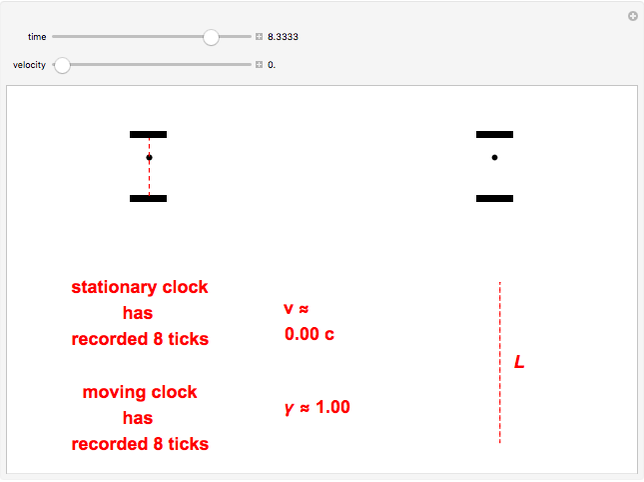
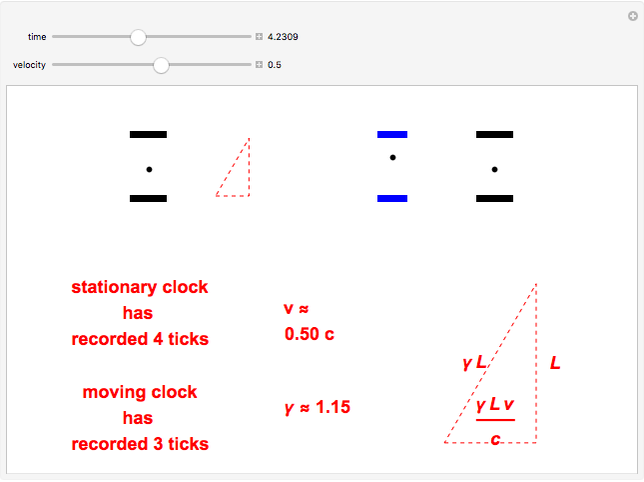
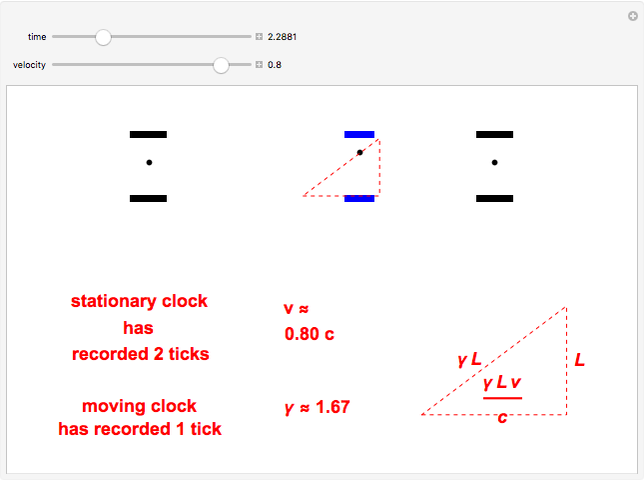
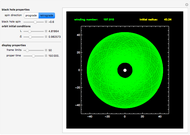
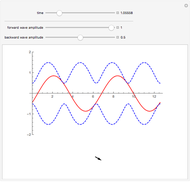
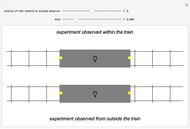
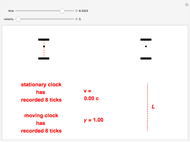
Time dilation is an intriguing implication of Einstein's special theory of relativity. The light clock is an elegant illustration of this effect, relying only on a knowledge of the Pythagorean theorem and the invariance of the speed of light.
[more]
Contributed by: Quentin Sedlacek (March 2011)
Based on a program by: Howard Georgi
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Light Clocks and Time Dilation"
http://demonstrations.wolfram.com/LightClocksAndTimeDilation/
Wolfram Demonstrations Project
Published: March 7 2011