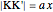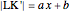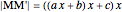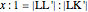Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Lill's Method for Calculating the Value of a Cubic Polynomial

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

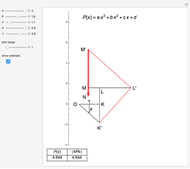
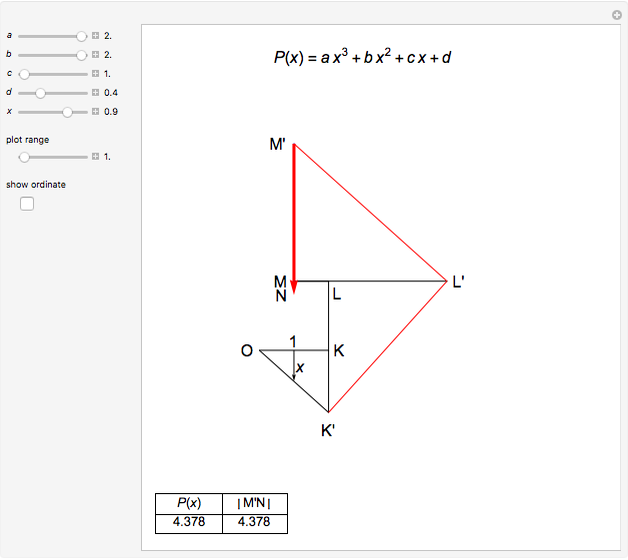
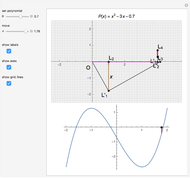
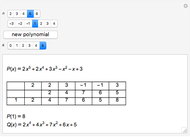
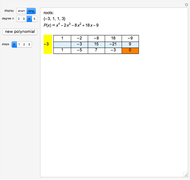
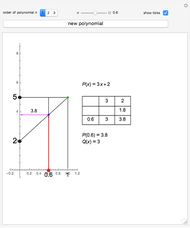
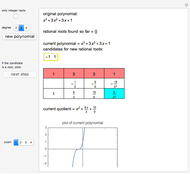
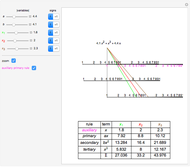
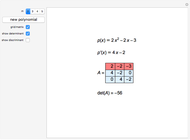
This Demonstration shows Lill's graphic method for calculating the value of a cubic polynomial 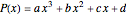using the Horner formulas:

[more]

,

,

,

,

,

and finally,

.

This is true by Thales's side-splitter theorem. For instance , .

[less]

Contributed by: Izidor Hafner (August 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This method is attributed to the French engineer Eduard Lill (1867).

The side-splitter theorem states: If a line parallel to one side of a triangle intersects the other two sides in different points, it divides the sides in the same ratio [2. p. 354].

References

[1] D. Kurepa, Higher Algebra (in Croatian), Zagreb: Skolska knjiga, 1965 pp. 1071–1073.

[2] H. R. Jacobs, Geometry (2nd ed.), New York: W. H. Freeman and Company, 1987.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send