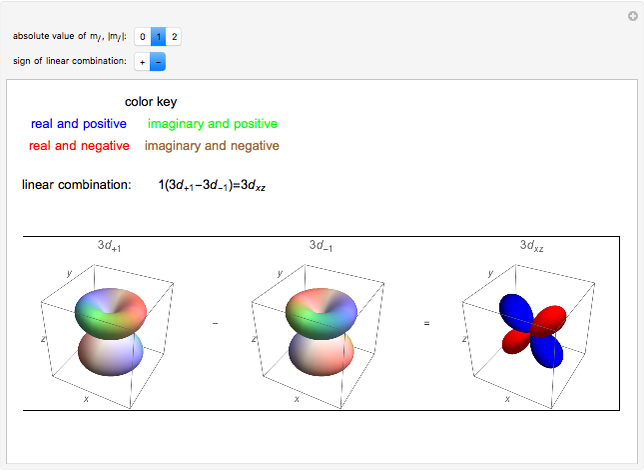
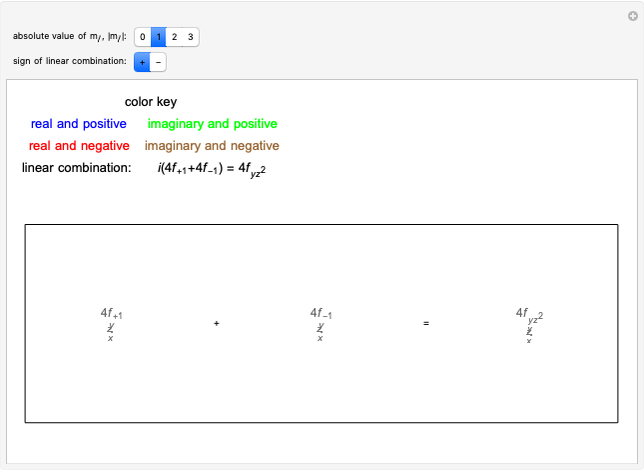
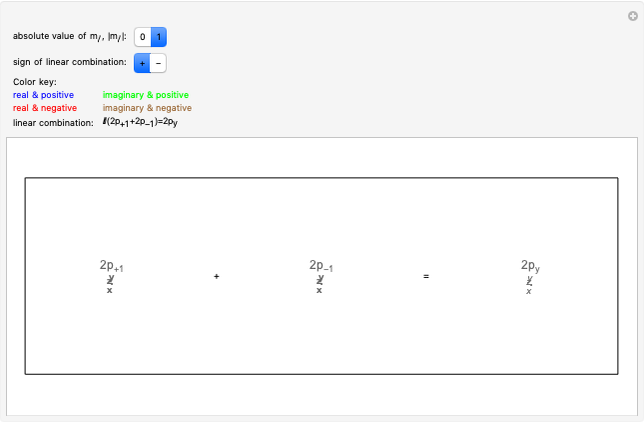
Linear Combinations of d Orbitals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
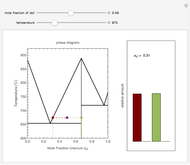
Chemistry students encountering  atomic orbitals for the first time often wonder why the
atomic orbitals for the first time often wonder why the 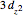 orbital looks so different from the others. The answer is related to the fact that boundary surface pictures of atomic orbitals typically show only the real part of these complex functions and often leave out the sign information as well. The one-electron wavefunctions resulting from the solution of the Schrödinger equation for the hydrogen atom are complex functions except when
orbital looks so different from the others. The answer is related to the fact that boundary surface pictures of atomic orbitals typically show only the real part of these complex functions and often leave out the sign information as well. The one-electron wavefunctions resulting from the solution of the Schrödinger equation for the hydrogen atom are complex functions except when 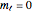 . The real forms of
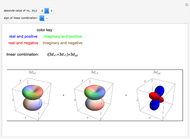
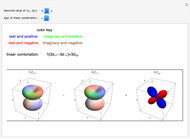
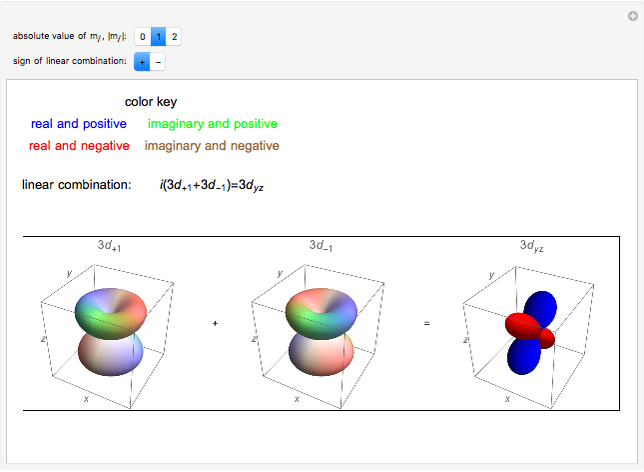
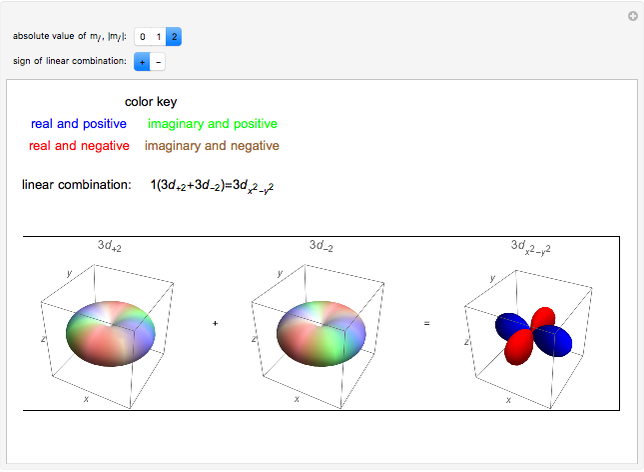
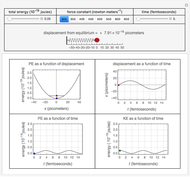
. The real forms of  atomic orbitals can be constructed by taking appropriate linear combinations of the complex forms. Here, boundary surfaces of the
atomic orbitals can be constructed by taking appropriate linear combinations of the complex forms. Here, boundary surfaces of the  orbitals are colored to indicate the real and imaginary components as well as the positive and negative signs. These color-coded atomic orbitals illustrate the linear combinations of the complex wavefunctions that result in the familiar four-lobe pictures.
orbitals are colored to indicate the real and imaginary components as well as the positive and negative signs. These color-coded atomic orbitals illustrate the linear combinations of the complex wavefunctions that result in the familiar four-lobe pictures.
Contributed by: Lisa M. Goss (March 2011)
Open content licensed under CC BY-NC-SA
Details
Snapshots
Permanent Citation