Lipschitz Continuity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
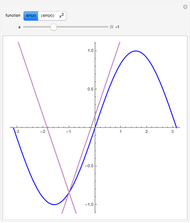
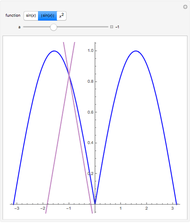
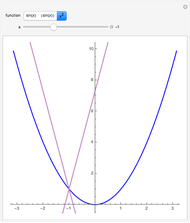
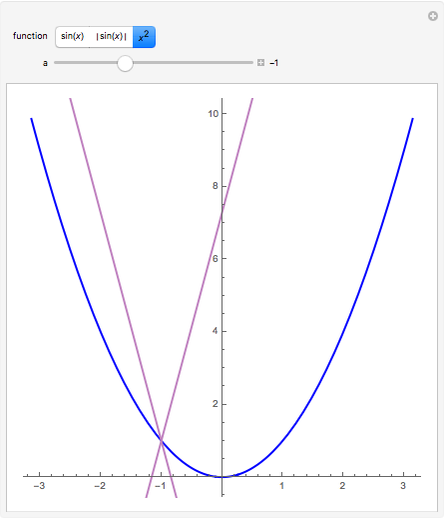
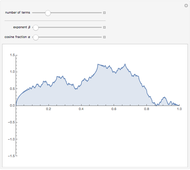
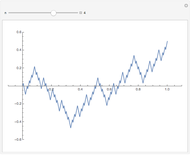
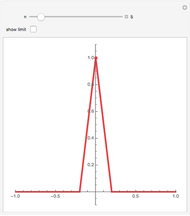
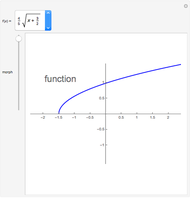
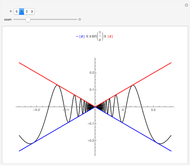
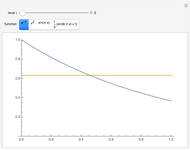
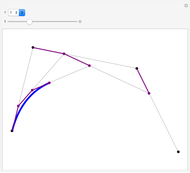
A function  is Lipschitz continuous on an interval if there is a positive constant
is Lipschitz continuous on an interval if there is a positive constant 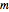 such that
such that 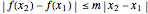 for all
for all 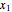 ,
,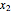 in the interval. Geometrically this requires the entire graph of
in the interval. Geometrically this requires the entire graph of 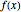 to be between the lines
to be between the lines 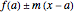 for any
for any  in the interval. The smallest possible
in the interval. The smallest possible 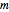 is the largest magnitude of the slope of
is the largest magnitude of the slope of 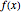 in the interval.
in the interval.
Contributed by: Bruce Atwood (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Lipschitz Continuity"
http://demonstrations.wolfram.com/LipschitzContinuity/
Wolfram Demonstrations Project
Published: March 7 2011