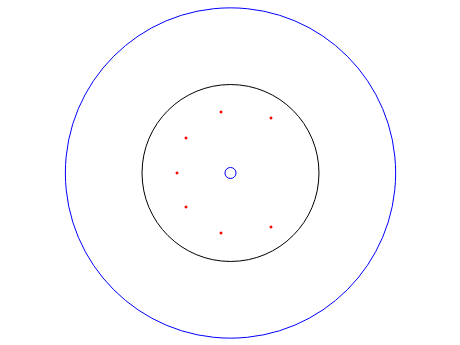
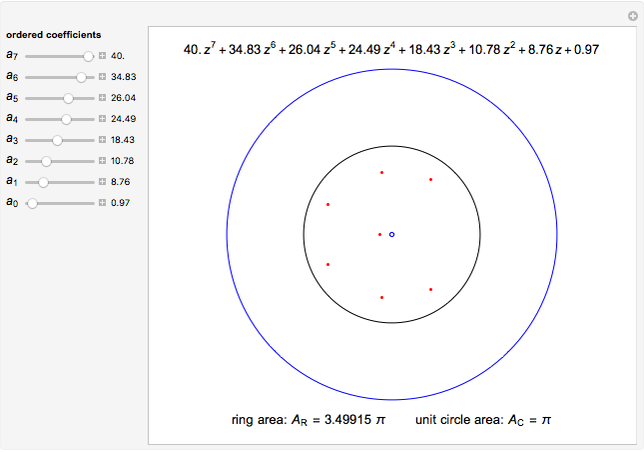
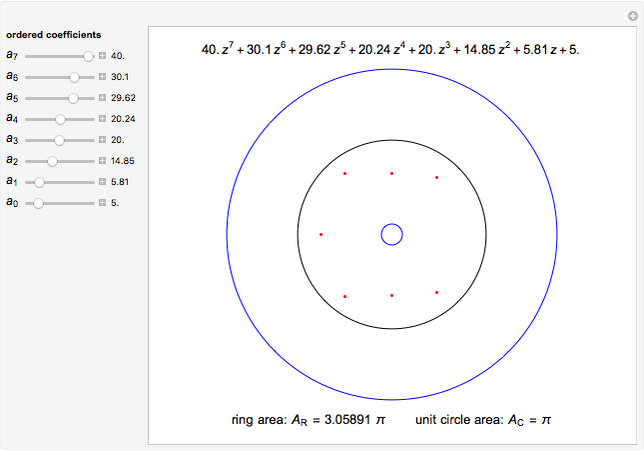
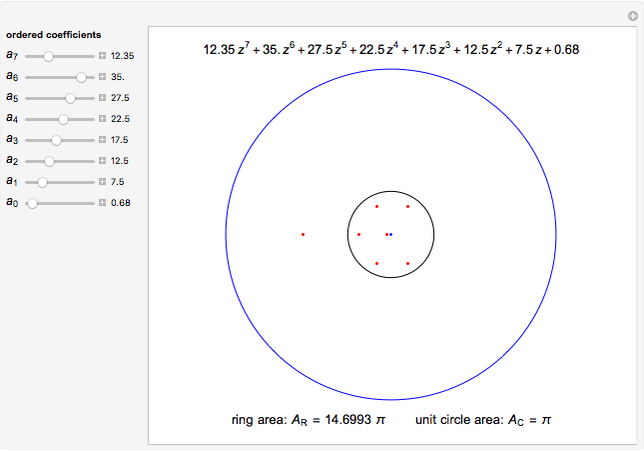
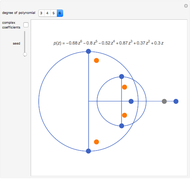
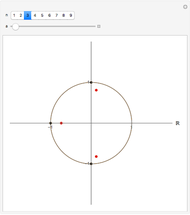
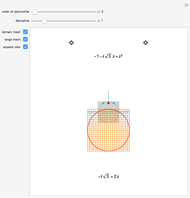
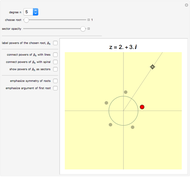
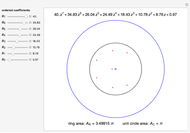
This Demonstration shows the location of the zeros of a polynomial 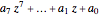of degree seven with positive coefficients. When the coefficients are ordered , the Eneström–Kakeya theorem states that the zeros (red points) lie in the unit circle, represented by the black circle centered in the origin. Furthermore, regardless of the order of the coefficients, the zeros lie in the ring 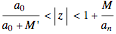, where 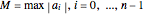and , represented by the blue circles centered in the origin.