Lorentz Transformation for a Rotating Square
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
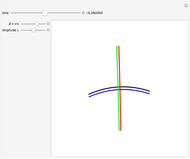
This Demonstration shows the deformation of a rotating square according to the Lorentz transformation from the frame of reference of a rocket (RFR) moving with a velocity  . Beta (
. Beta (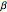 ) is the ratio
) is the ratio  , where
, where  is the speed of light, so
is the speed of light, so 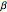 goes from 0 to 1.
goes from 0 to 1.
Contributed by: Carlos Anton Solanas (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
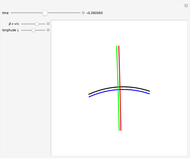
Snapshot 1: a rotating cross with the RFR at rest ( )
)
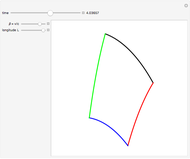
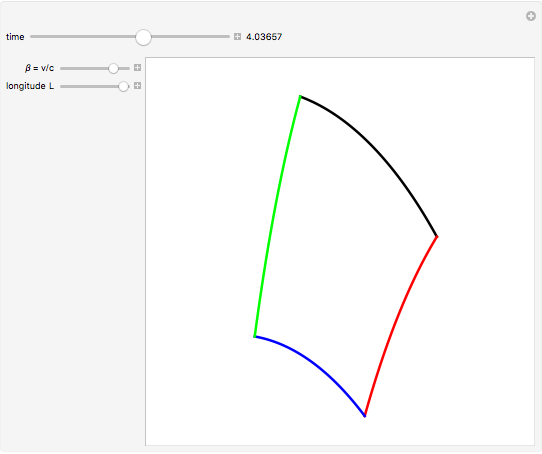
Snapshot 2: by increasing 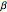 , the square changes shape
, the square changes shape
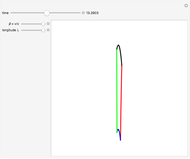
Snapshot 3: in the limit as  , the square becomes a vertical line, according to the Lorentz contraction
, the square becomes a vertical line, according to the Lorentz contraction
Permanent Citation