Lorentz Transformation for Twin Paradox

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
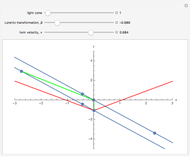
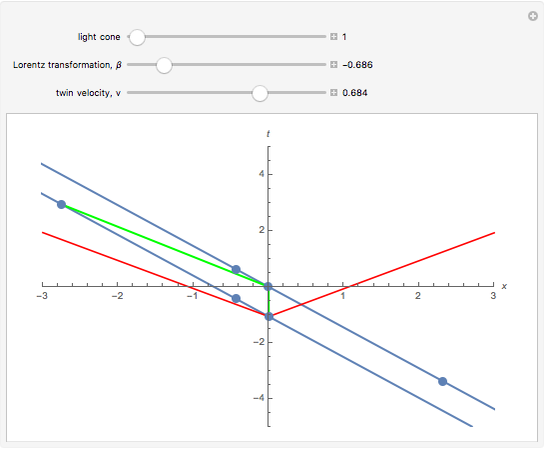
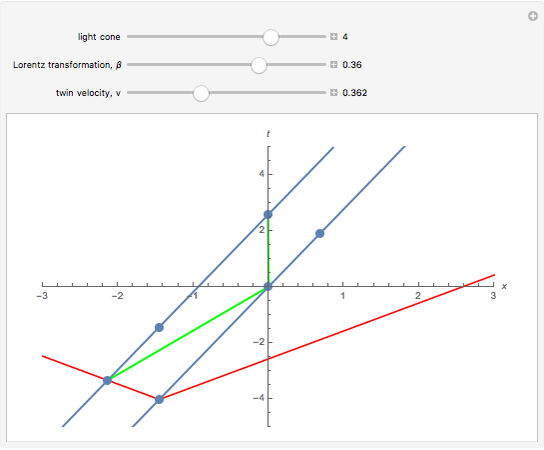
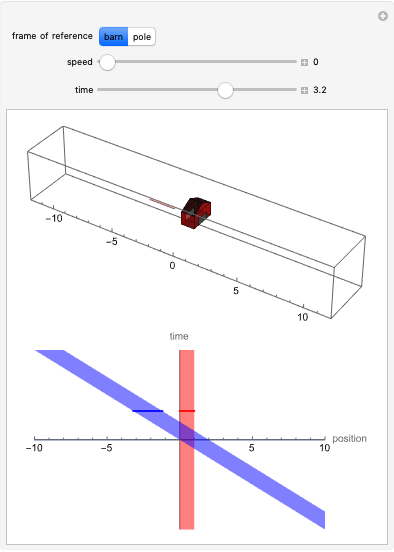
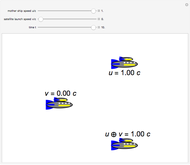
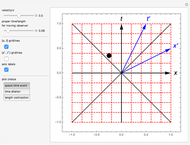
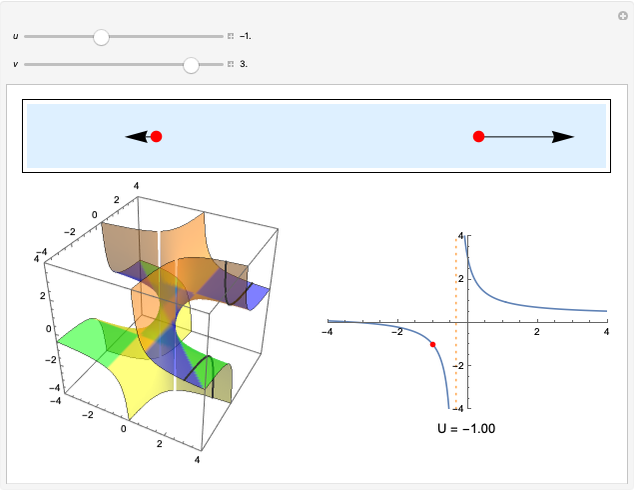
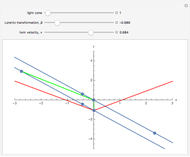
The much-cited twin paradox consists of three stages: (1) the traveling twin takes off; (2) he turns around; and (3) he arrives back home. Those three events are connected by the green line segments. In this simulation, imagine that the traveling twin is moving between two walls or space stations, with the path marked in blue. The presence of these two space stations suggests three more observable events, namely, what can be seen happening at the opposite space station by the traveling twin when he is at: (4) takeoff; (5) turnaround; and (6) arrival home. You can adjust the light cone parameter to the viewpoint of each of these six events, and adjust the "beta" parameter, to see the space-time diagram in different reference frames.
Contributed by: Jonathan Doolin (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The scale of the  and
and  axes is not given, but you may choose light-seconds and seconds or light-years and years, and so on. To see the space-time diagram for the right-bound trip, make the lower (green) leg of the trip vertical. Then for the left-bound trip, adjust the upper (green) leg of the trip to be vertical. The vertical distance between events represents the time experienced by each observer. You can see the time experienced by the stay-at-home twin by making the blue line vertical. When both legs of the twin's journey (green) are successively made vertical, you can see that the total time elapsed for the traveling twin is less than that for the stay-at-home twin. Of particular interest is the perceived distance to the opposite space station, which depends on the velocity of the twin. This phenomenon is commonly called "aberration" and is described as a shrinking of the image in the direction of acceleration. However, the actual phenomenon is not a mere shrinking of an image, but an actual increase in the distance to the visible event. As objects approach the speed of light, the image appears to move faster than the speed of light, because the light from the object arrives only shortly before the object itself. This phenomenon is called "superluminal motion".
axes is not given, but you may choose light-seconds and seconds or light-years and years, and so on. To see the space-time diagram for the right-bound trip, make the lower (green) leg of the trip vertical. Then for the left-bound trip, adjust the upper (green) leg of the trip to be vertical. The vertical distance between events represents the time experienced by each observer. You can see the time experienced by the stay-at-home twin by making the blue line vertical. When both legs of the twin's journey (green) are successively made vertical, you can see that the total time elapsed for the traveling twin is less than that for the stay-at-home twin. Of particular interest is the perceived distance to the opposite space station, which depends on the velocity of the twin. This phenomenon is commonly called "aberration" and is described as a shrinking of the image in the direction of acceleration. However, the actual phenomenon is not a mere shrinking of an image, but an actual increase in the distance to the visible event. As objects approach the speed of light, the image appears to move faster than the speed of light, because the light from the object arrives only shortly before the object itself. This phenomenon is called "superluminal motion".
Permanent Citation
"Lorentz Transformation for Twin Paradox"
http://demonstrations.wolfram.com/LorentzTransformationForTwinParadox/
Wolfram Demonstrations Project
Published: March 7 2011