Low-Pass and High-Pass Filtering of Images
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
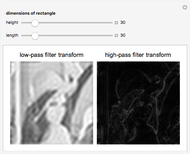
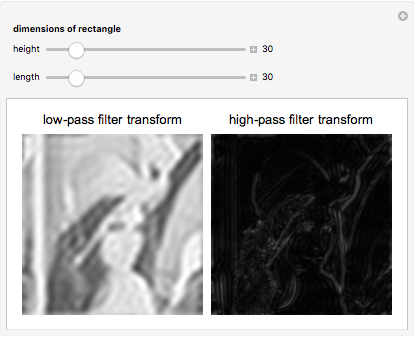
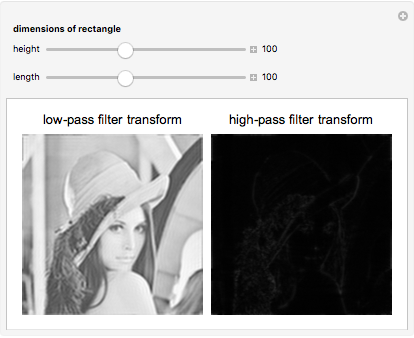
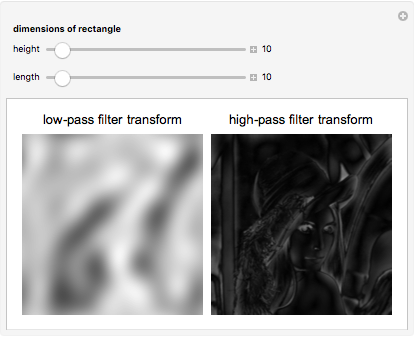
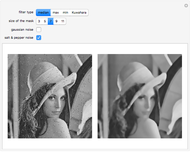
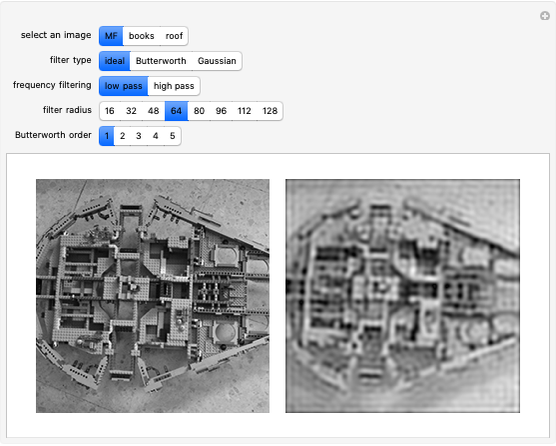
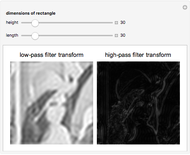
This Demonstration shows the results of applying two different types of filters to images. To apply the filters, the discrete Fourier transform of the image is taken and then changed through a series of steps. The filter is then applied by performing pointwise multiplication with the transform matrix and the rectangular filter that cancels out high frequencies if it is a high-pass filter or low frequencies if a low-pass filter. The steps are then done in inverse, and then the inverse discrete Fourier transform is taken to give the result. Notice that when low frequencies closer to the center are filtered out, there is more blurring at areas of rapidly changing pixel intensity, and when high frequencies closer to the edges are filtered, the areas of rapidly changing intensity are emphasized to show an outline of the image.
Contributed by: Krishnan Chander (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
These are the steps that the program conducts to output the results:
1. Read in the image as a pixel intensity matrix.
2. Take the fast Fourier transform of the matrix. To obtain a power spectrum, multiply each element of the transform matrix by its complex conjugate.
3. Take the base-2 logarithm of each element of the power spectrum in order to improve its brightness and contrast settings in the display.
4. Shift the result's zero-frequency component from the top-left corner to the center by splitting the matrix into four equally sized quadrants and swapping them across the center.
5. Create a low-pass filter by making a rectangle of 1's, with the dimensions specified by the manipulated variables, at the center of a matrix of 0's with the same dimensions as the image. To make a high-pass filter, make the rectangle full of 0's among a matrix of 1's.
6. Multiply the shifted logarithm of the power spectrum by each filter pointwise.
7. Apply all the steps to change the power spectrum inversely to the filtered results. Then divide them by the complex conjugate matrix of the Fourier transform of the image.
8. Perform a fast inverse Fourier transform on the results.
9. Output the absolute value of the inverse transforms as images.
Permanent Citation
"Low-Pass and High-Pass Filtering of Images"
http://demonstrations.wolfram.com/LowPassAndHighPassFilteringOfImages/
Wolfram Demonstrations Project
Published: March 7 2011
Nonlinear Image Filtering
José A. Díaz
Filtering Images in the Frequency Domain
José A. Díaz
Image Kernels and Convolution (Linear Filtering)
Hector Sanchez
Finding Segments of an Image by Filtering Its Distance Transform
Shadi Ashnai
Image Jitter Filter
Shadi Ashnai
Sharpening Images
José A. Díaz
Resizing Images
Yu-Sung Chang
Gaussian Filtering for Blurring
Srivani Pinneli and Yu-Sung Chang
Geometric Mean Filtering for Blurring
Srivani Pinneli
Filtering Using Common Value
Srivani Pinneli
