Lubricated and Frictional Squeezing Flow

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
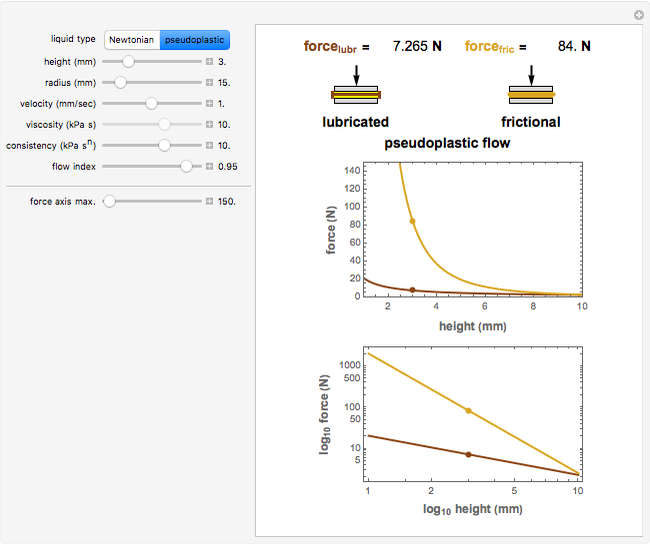
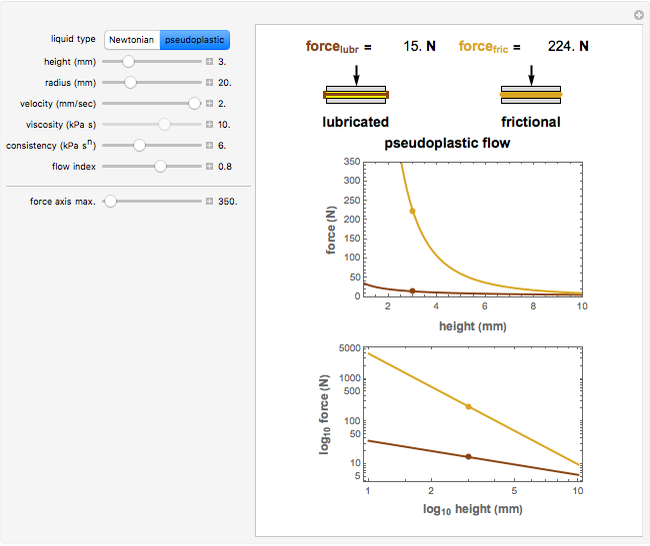
This Demonstration illustrates the theoretical roles that friction, geometry, and rheological properties of a liquid play in idealized squeezing flow between perfectly parallel plates. It calculates and displays the force for Newtonian and pseudoplastic liquids compressed at different deformation rates in lubricated (frictionless) and frictional modes. It also plots the corresponding force versus height relationship on both linear and logarithmic coordinates.
Contributed by: Mark D. Normand and Micha Peleg (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
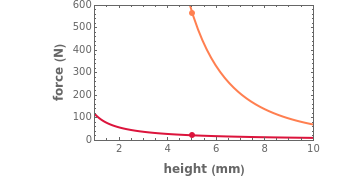
Snapshot 1: an almost Newtonian liquid between "narrow" plates
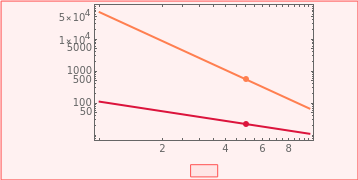
Snapshot 2: a highly pseudoplastic liquid between "wide" plates
Snapshot 3: a moderately pseudoplastic liquid between "narrow" plates
The purpose of this Demonstration is to illustrate the effects of the rheological properties, geometry, friction, and test conditions on the force versus height relationship in squeezing flow viscometry of semi-liquid foods and other materials. This is done by using published theoretical equations developed for specimens compressed between lubricated and nonlubricated parallel plates. The variables are the specimens momentary height,  (in mm), the plate's radius,
(in mm), the plate's radius,  (in mm), the upper-plate velocity,
(in mm), the upper-plate velocity,  (in mm/s), the specimen's viscosity when Newtonian,
(in mm/s), the specimen's viscosity when Newtonian,  (in kPa s), or when pseudoplastic, its consistency,
(in kPa s), or when pseudoplastic, its consistency,  (in kPa
(in kPa 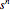 ) and dimensionless flow index,
) and dimensionless flow index,  , all entered with sliders.
, all entered with sliders.
Two equations are used for Newtonian liquids: for ideal frictionless plug flow 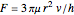 and for ideal frictional flow
and for ideal frictional flow 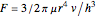 .
.
Two equations are used for pseudoplastic liquids: for ideal frictionless plug flow, 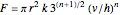 and for ideal frictional flow,
and for ideal frictional flow, 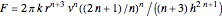 .
.
The liquid type, Newtonian or pseudoplastic, is chosen with a setter bar. The display includes the numerical force values for the lubricated and frictional modes, schematic drawings of the plates' diameter and positions (not to scale), and plots of the force versus height relationship on linear and logarithmic coordinates. The upper limit of the logarithmic plot's force axis is set automatically, while that of the linear plot can be adjusted with a slider.
References:
S. J. Lee, M. M. Denn, M. J. Crochet, and A. B. Metzner, "Compressive Flow Between Parallel Discs," Journal of Non-Newtonian Mechanics, 10, 1982 pp. 3–20.
S. H. Chatraei, C. W. Macosko, and H. H. Winter, "Lubricated Squeezing Flow: A New Biaxial Extensional Rheometer," Journal of Rheology, 25, 1981 pp. 433–443.
P. J. Leider and B. R. Bird, "Squeezing Flow Between Parrallel Disks," Industrial Engineering Chemistry Fundamentals, 13, 1974 pp. 336–341.
E. M. Casiraghi, E. B. Bagley, and D. D. Christianson, "Behavior of Mozarella, Cheddar and Processed Cheese Spread in Lubricated and Bonded Compression," Journal of Texture Studies, 16, 1985 pp. 281–301.
O. H. Campanella and M. Peleg, "Squeezing Flow Viscosimetry of Peanut Butter," Journal of Food Science, 52, 1987 pp. 180–184.
Permanent Citation