Magic Squares and Designs

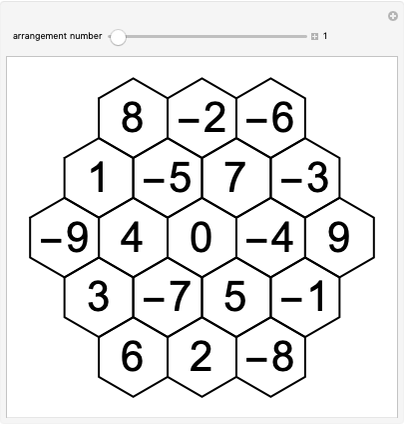
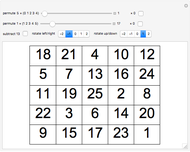
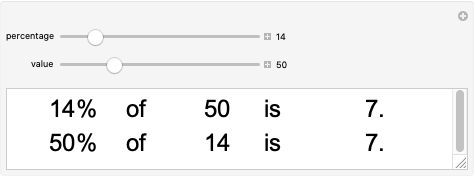
There are 880 4×4 magic squares, where each row, column, and diagonal adds up to 34. Two squares are shown—the one on the left is magic—below each one, a line shows the route of 1 to 2 to 3 and so on.

In the two squares, there are 20 quadruples in the rows, columns, and main diagonals. Choose any pair of numbers from 1 to 16. The chosen pair will appear exactly once on a row, column, or main diagonal of one of the two squares. This gives a combinatorial design: the Steiner quadruple system 2-{16,4,1}, also called a t-design. The 2 is for pairs, 16 is the number of symbols, in groups of 4, each pair appearing exactly 1 time.