Magnetization Using an Ising Model Based on a Search-Update-Feedback Cellular Automata (SCA) Approach

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
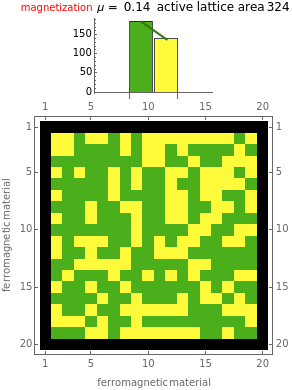
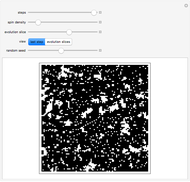
This Demonstration deals with the electron-spin alignment dynamics inherent in ferromagnetic material. A persistent macroscopic magnetization is manifested when the material's initial spin densities are such that one of these spin phases is sufficiently greater than the other. The default spin-down density setting of 0.5, which translates to a complement spin-up density of 0.5, therefore rarely manifests any magnetization.
Contributed by: Michael Dewus (July 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Physics Background
Electron spin, when sufficiently aligned, catalyzes macroscopic magnetization; this is probably a good summary of this Demonstration. In ferromagnetic material, a quantum-mechanical mechanism, the exchange interaction, predominantly forces electron spin alignment. The spin-discretization inherent in the Ising model together with the Q2R rule employed by the SCA are used to model this mechanism. The electrons are unpaired outer valence electrons of adjacent atoms, and the ferromagnetic material containing them is assumed to be below its Curie temperature; moreover, it is assumed that there is no external magnetic field acting upon the material.
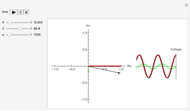
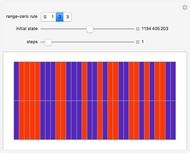
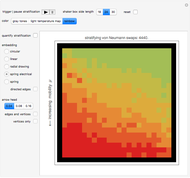
In the energy diagram just below, 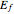 is some zero-referenced Fermi level of the ferromagnetic material—in the Demonstration this critical bulk (macroscopic) potential energy is realized at magnetization, and has energetically moved down from 0 potential energy (the initial lattice is comprised of a random spin-align orientation, as in the thumbnail and first snapshot, which is consistent with 0 potential energy and no net magnetization; isdd =0.5 here), and commensurately up from
is some zero-referenced Fermi level of the ferromagnetic material—in the Demonstration this critical bulk (macroscopic) potential energy is realized at magnetization, and has energetically moved down from 0 potential energy (the initial lattice is comprised of a random spin-align orientation, as in the thumbnail and first snapshot, which is consistent with 0 potential energy and no net magnetization; isdd =0.5 here), and commensurately up from  potential energy. When
potential energy. When 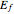 is realized, electron-spin aligning activity (which is spin magnetic moment growth equal to
is realized, electron-spin aligning activity (which is spin magnetic moment growth equal to  , shown in the plot label) ceases, because nature's potential energy dynamics definitive,
, shown in the plot label) ceases, because nature's potential energy dynamics definitive,  , has been entirely satisfied; the equation states that the forces act in such a way as to lower potential energy. In practice, and in accord with the equation, electrons lower their electrostatic potential energy by aligning their spins, because this maximizes the separation between them as a consequence of the repulsive electrostatic forces acting in the aligned configuration. In turn, this maximized outer electron separation that pervades the lattice gives rise to the beautiful electron spatial symmetry and order characteristic of ferromagnetic material. Once this maximum electron separation is forced,
, has been entirely satisfied; the equation states that the forces act in such a way as to lower potential energy. In practice, and in accord with the equation, electrons lower their electrostatic potential energy by aligning their spins, because this maximizes the separation between them as a consequence of the repulsive electrostatic forces acting in the aligned configuration. In turn, this maximized outer electron separation that pervades the lattice gives rise to the beautiful electron spatial symmetry and order characteristic of ferromagnetic material. Once this maximum electron separation is forced, 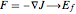 is satisfied, and ideally spin-magnetic moment growth ceases because
is satisfied, and ideally spin-magnetic moment growth ceases because 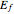 cannot be intrinsically driven any lower toward saturation. Attaining this stable magnetic moment is realized as a form of macroscopic magnetization—that is why electron spin stabilization is this Demonstration's magnetization arbitrator. A plot label
cannot be intrinsically driven any lower toward saturation. Attaining this stable magnetic moment is realized as a form of macroscopic magnetization—that is why electron spin stabilization is this Demonstration's magnetization arbitrator. A plot label  reading of
reading of  is perfectly stationary magnetic moment growth; the Demonstration considers
is perfectly stationary magnetic moment growth; the Demonstration considers  readings of
readings of 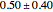 to be the condition for macroscopic magnetization—this window was determined by lobe prominence observations consequent to quantifying the matrix plot simulation as explained below.
to be the condition for macroscopic magnetization—this window was determined by lobe prominence observations consequent to quantifying the matrix plot simulation as explained below.
Bulk Material Energy Diagram
 : spin-magnetic moment growth—expansion or contraction
: spin-magnetic moment growth—expansion or contraction
0: random electron spin alignment (ideally,  here)
here)
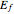 : magnetization (ideally,
: magnetization (ideally, 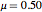 here)
here)
 : saturation-complete electron spin alignment (ideally,
: saturation-complete electron spin alignment (ideally, 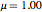 here)
here)
For more physics information, see the Wikipedia entries for antiferromagnetism, Curie temperature, diamagnetism, exchange interaction, ferromagnetism, ferrimagnetism, Ising model, magnetic moment, magnetism, Néel temperature, and paramagnetism.
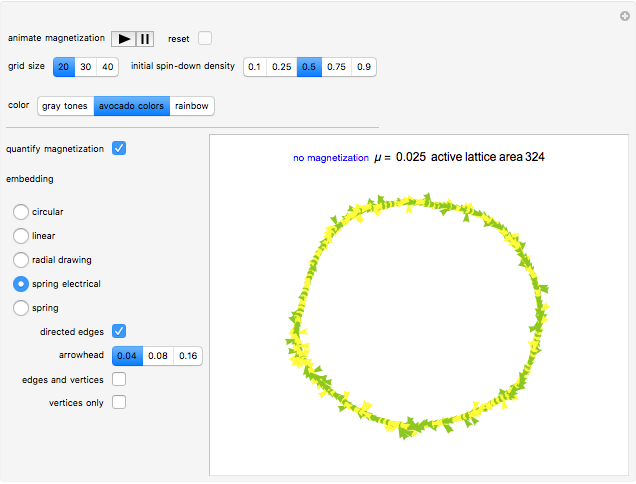
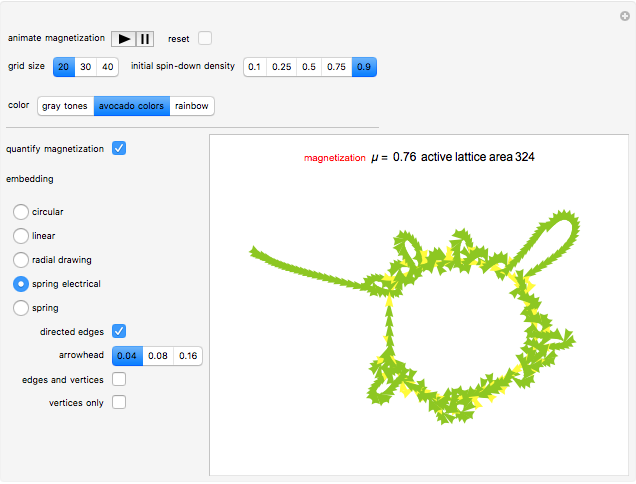
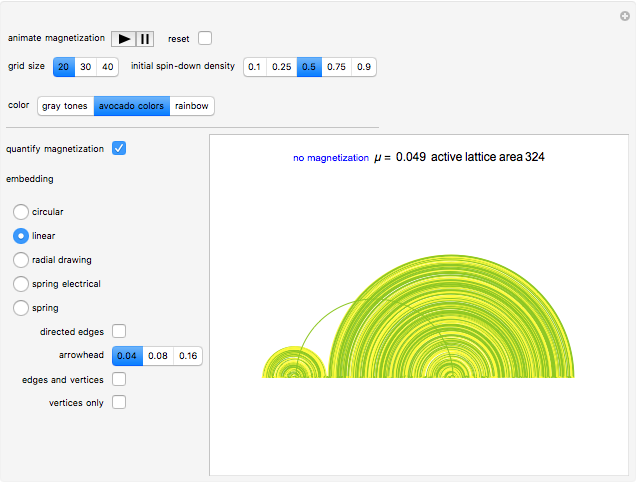
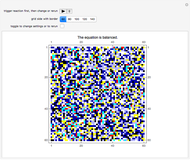
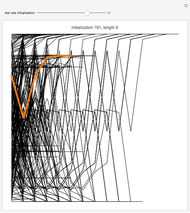
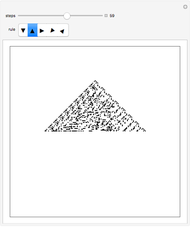
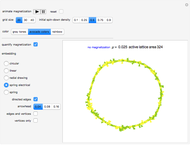
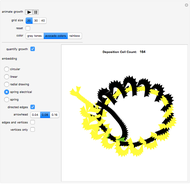
The control "animate magnetization" initiates and pauses the local energy checks that either flip or keep unchanged a given electron spin state—in this check, when the automaton senses that flipping a given electron spin state conserves local (automaton neighborhood) energy, the spin flips to its opposite state. Use the "quantify magnetization" control to switch between the matrix plot simulation and the network quantification; the latter shows the causal relationship between electron spin flips and macroscopic magnetization and it quantifies the simulation. With respect to spring electrical-embedding, a flattening of lobes suggests spin alignment randomization, while prominent lobing indicates preferential spin alignment (compare the first and second snapshots). Watch also for lobe interplay, which reflects subtle spatial changes in magnetization; lobe interplay would be consistent with electron spin aggregation in the matrix plot. Use the "reset" control to change the lattice size and initial spin densities.
Search-Update-Feedback Cellular Automata (SCA) Background
Active cell (AC) and neighborhood (NHD): The SCA NHD can take any shape—curvilinear or hybrid—that satisfies the objective at hand, and the AC need not be a neighborhood center cell.
Perhaps the real beauty of SCA lies in the easy computational accessibility and tracking of the AC or NHD in both time and space, and the rich modeling possibilities that emerge from that computational versatility. Mathematica nesting iterators easily locate AC/NHD in time (see for example the Demonstration "2D Heat Diffusion, an SCA Approach"), and most any method locates AC/NHD in space (this code locks in the spatial possibilities; other methods have been employed; SCA search speed is of consideration here).
Updating: SCA updating is neither synchronous nor sequential, it is random, the motivating assumption being that nature is not perfectly synchronous or sequential in its updating. SCA are very natural in that regard in many applications, owing to the random updating driven by recursion that itself forces near-environment updating for as long as the environment will allow updating to persist.
References
[1] M. R. Wehr, J. A. Richards, and T. A. Adair III, Physics of the Atom, Reading, MA: Addison–Wesley, 1978.
[2] B. Chopard and M. Droz, Cellular Automata Modeling of Physical Systems, Cambridge: Cambridge University Press, 2005.
[3] Wikipedia, "Feedback." (Jan 12, 2014)en.wikipedia.org/wiki/Feedback
Permanent Citation