Magnified Views of the Mandelbrot Set

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The Mandelbrot set is defined as the collection of points  in the complex plane for which the orbit of the iterated relation
in the complex plane for which the orbit of the iterated relation  , known as the Julia set for
, known as the Julia set for  , remains in a finite, simply connected region as
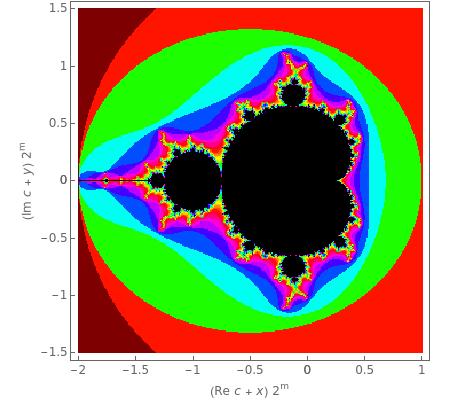
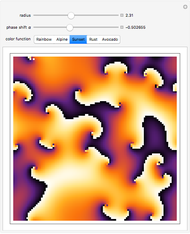
, remains in a finite, simply connected region as  . The Mandelbrot set, which has a fractal boundary, is shown in black on the graphic. Two dominant features are a cardioid and a circular disc tangent to one another. If
. The Mandelbrot set, which has a fractal boundary, is shown in black on the graphic. Two dominant features are a cardioid and a circular disc tangent to one another. If  for any value of
for any value of  , then the point cannot belong to the Mandelbrot set. Such points fall in a colored region, with different colors determined by the number of steps it takes for an orbit to reach a value
, then the point cannot belong to the Mandelbrot set. Such points fall in a colored region, with different colors determined by the number of steps it takes for an orbit to reach a value  . Magnification of various regions of the complex plane reveals an incredible variety of fractal structures. The classic computer-generated images were published by Peitgen and Richter (The Beauty of Fractals: Heidelberg, Springer-Verlag, 1986). This Demonstration cannot reproduce their computational power, but a general idea of the richness of the Mandelbrot set can be obtained with magnifications up to
. Magnification of various regions of the complex plane reveals an incredible variety of fractal structures. The classic computer-generated images were published by Peitgen and Richter (The Beauty of Fractals: Heidelberg, Springer-Verlag, 1986). This Demonstration cannot reproduce their computational power, but a general idea of the richness of the Mandelbrot set can be obtained with magnifications up to  with 300×300-pixel resolution. The 2D slider centers the image on a desired region for magnification. The magnification should be increased stepwise for optimal control.
with 300×300-pixel resolution. The 2D slider centers the image on a desired region for magnification. The magnification should be increased stepwise for optimal control.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
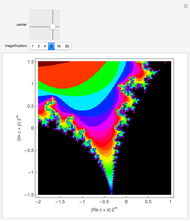
Snapshot 1: the region between the two main features is known as "seahorse valley"
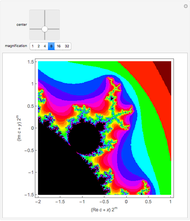
Snapshot 2: each circular disk grows smaller circular disks; "baby Mandelbrot sets" also appear
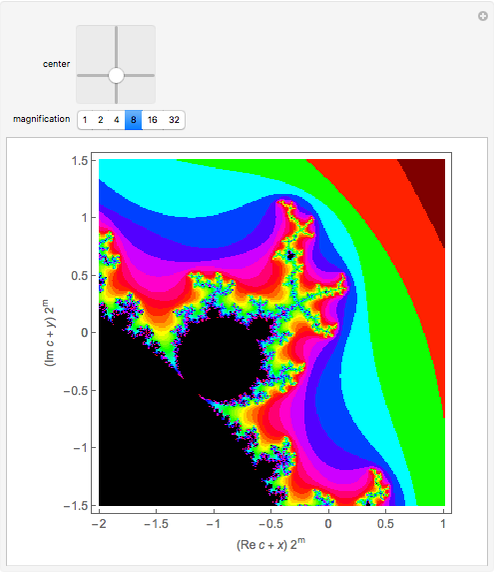
Snapshot 3: one of many remarkably complex fractal patterns under higher magnification
A selection of Peitgen and Richter's images is shown in a Wikipedia article.
Permanent Citation
"Magnified Views of the Mandelbrot Set"
http://demonstrations.wolfram.com/MagnifiedViewsOfTheMandelbrotSet/
Wolfram Demonstrations Project
Published: March 7 2011