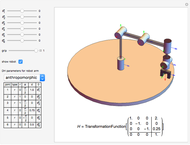
Manipulability Ellipsoid of a Robot Arm

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
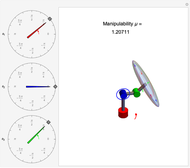
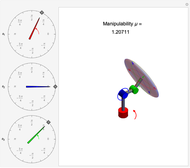
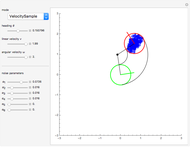
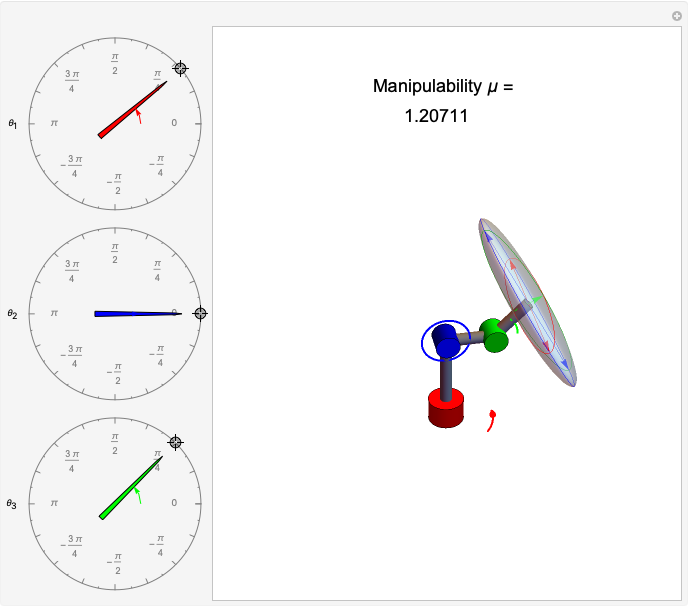
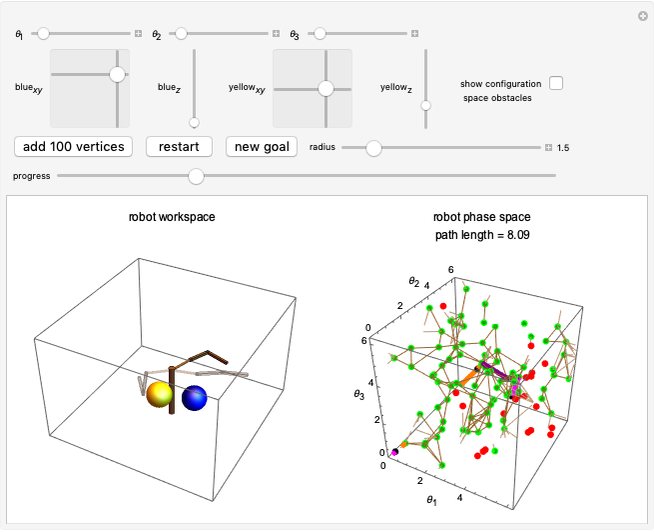
Manipulability of a robot is the capacity to change the end effector's position as a function of the joint configuration [1]. A larger manipulability measure indicates a greater range of possible motions at that configuration. The manipulability measure reduces to zero when the robot is in a singular configuration and cannot generate velocities in at least one direction.
[more]
Contributed by: Aaron T. Becker and Mary Burbage (June 2016)
Open content licensed under CC BY-NC-SA
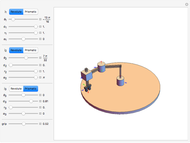
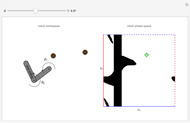
Snapshots
Details
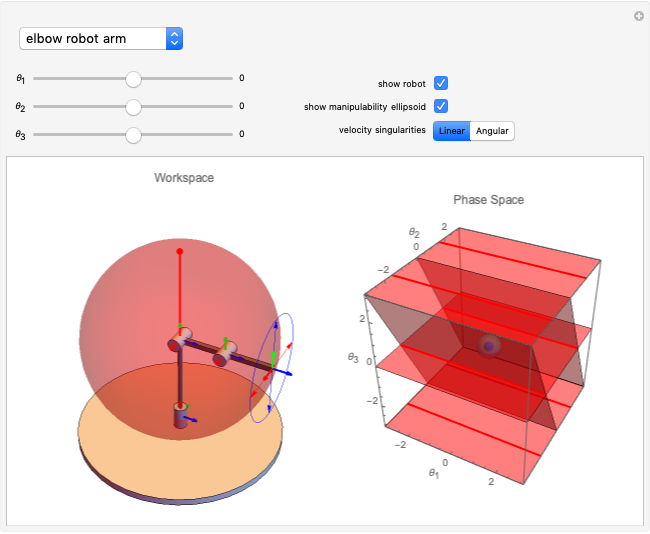
Calculating the manipulability requires defining the robot configuration in terms of joint angles (forward kinematics) and then calculating how joint velocities generate velocity of the end effector (velocity kinematics).
The configuration is defined using transformation matrices derived using the Denavit–Hartenberg convention. The three joints of the elbow manipulator allow three positional degrees of freedom, and the location (origin) of each joint is determined from these transformation matrices. These origins are combined with the axes of rotation from the same transformation matrices to develop the velocity Jacobian, which relates the end effector velocity to the rate of change in the joint positions. The velocity Jacobian 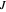 used in this Demonstration is given in [2, eq. 4.98, p. 144]. It is a function of the rotational position of each of the three joints, described by the variables
used in this Demonstration is given in [2, eq. 4.98, p. 144]. It is a function of the rotational position of each of the three joints, described by the variables 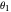 ,
, 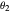 , and
, and 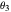 .
.
The velocity Jacobian is 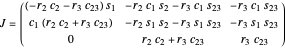 ,
,
where 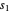 is shorthand for
is shorthand for 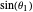 ,
,  is shorthand for
is shorthand for 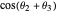 , and so on, and the lengths of links 2 and 3 are
, and so on, and the lengths of links 2 and 3 are 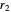 and
and  .
.
The manipulability measure is calculated as the product of the diagonal elements  in the
in the  matrix that results from the singular value decomposition of the velocity Jacobian,
matrix that results from the singular value decomposition of the velocity Jacobian, 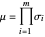 . It may also be defined relative to the determinant of the Jacobian as
. It may also be defined relative to the determinant of the Jacobian as 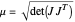 . From this definition, it is clear that
. From this definition, it is clear that 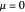 when the determinant of the Jacobian is zero. This occurs when the manipulator is in a singular configuration. The determinant of the Jacobian is
when the determinant of the Jacobian is zero. This occurs when the manipulator is in a singular configuration. The determinant of the Jacobian is 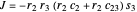 . When the elbow manipulator is in the configuration
. When the elbow manipulator is in the configuration 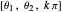 ,
, 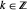 , the Jacobian has rank 2, and the three-dimensional ellipsoid flattens to a two-dimensional ellipse. At the configuration
, the Jacobian has rank 2, and the three-dimensional ellipsoid flattens to a two-dimensional ellipse. At the configuration 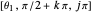 ,
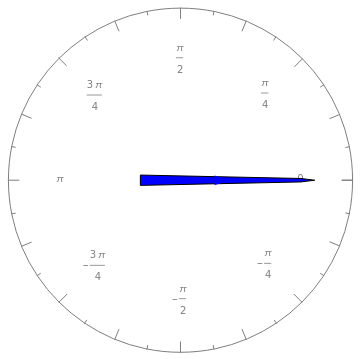
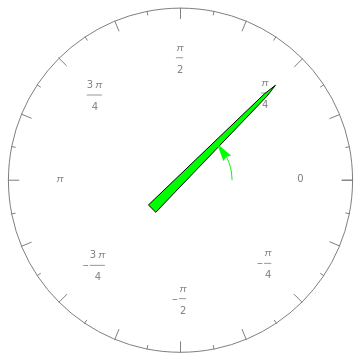
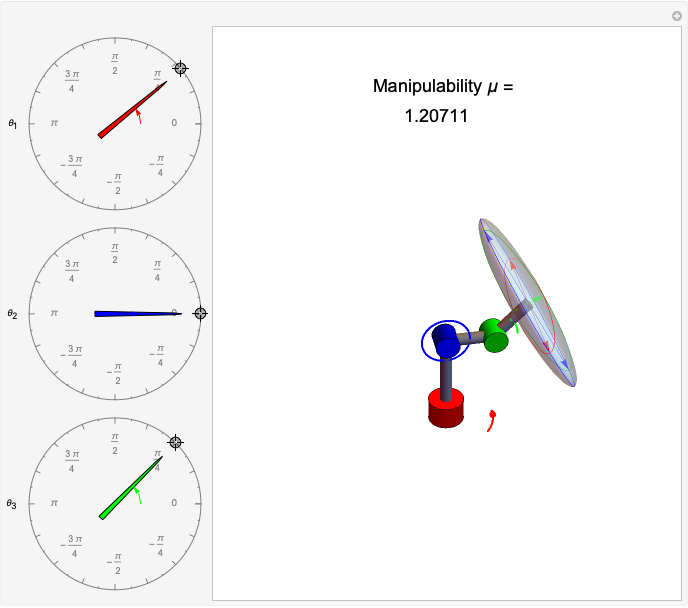
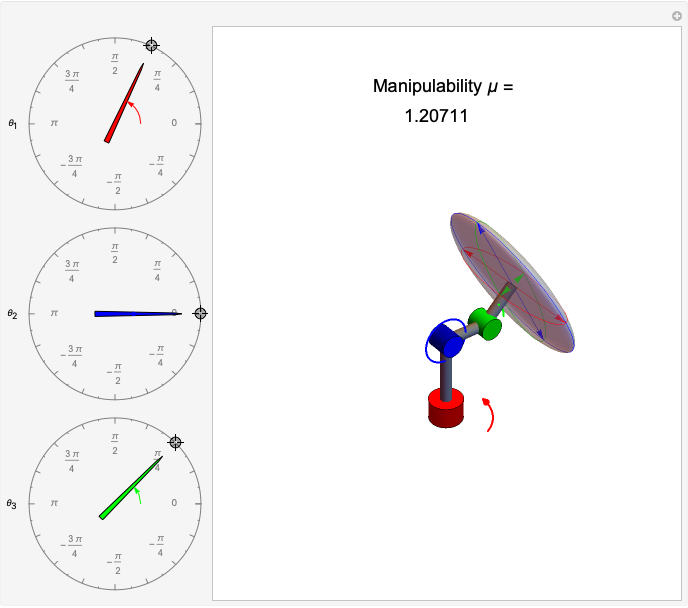
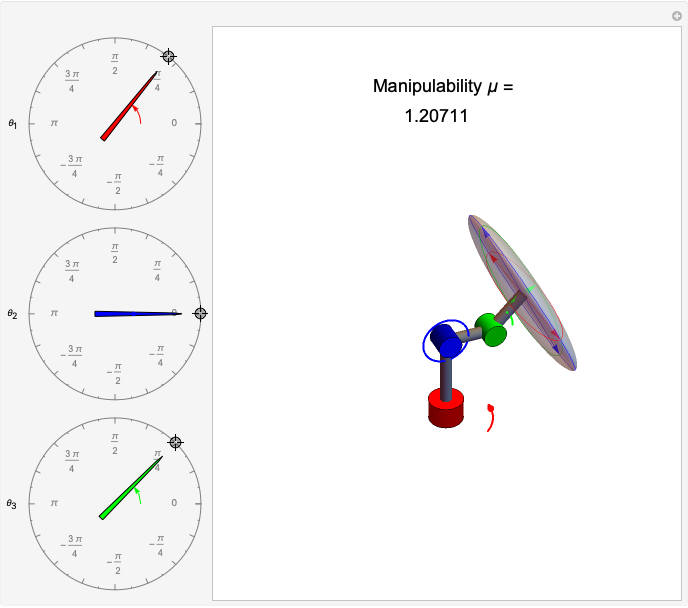
, 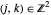 , the Jacobian has rank 1, and the ellipsoid collapses to a line. Snapshot 1 gives a three-dimensional ellipse, snapshot 2 a two-dimensional ellipse, and snapshot 3 a one-dimensional ellipse.
, the Jacobian has rank 1, and the ellipsoid collapses to a line. Snapshot 1 gives a three-dimensional ellipse, snapshot 2 a two-dimensional ellipse, and snapshot 3 a one-dimensional ellipse.
References
[1] J. Martinez, "Manipulability Ellipsoids in Robotics," Engineer JAU (blog). (May 26, 2016) engineerjau.wordpress.com/2013/05/04/advanced-robotics-manipulability-ellipsoids.
[2] M. W. Spong, S. Hutchinson, and M. Vidyasagar, Robot Modeling and Control, Hoboken, NJ: John Wiley and Sons, 2006.
Permanent Citation