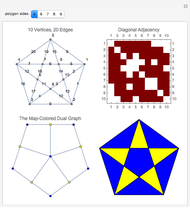
Map-Coloring the Interior Regions Defined by the Diagonals of a Regular Polygon

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
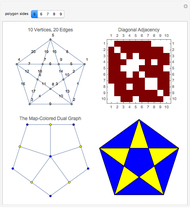
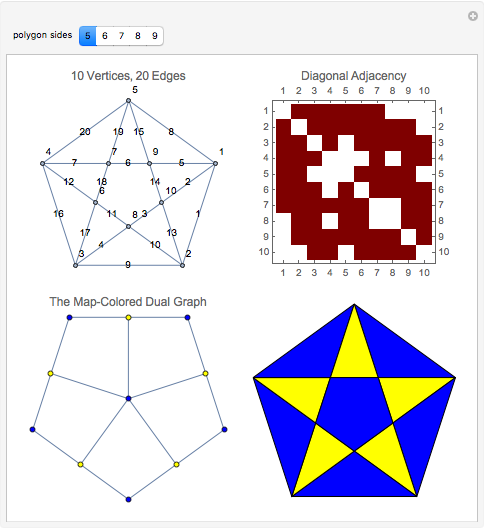
Graph-coloring the interior regions determined by the diagonals of a regular polygon is a simply stated but deceptively complex problem. Given a polygon with  sides, the number of diagonals increases at a rate between
sides, the number of diagonals increases at a rate between  and
and 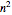 . The number of intersections between diagonals and the number of interior regions increase at a super-cubic rate
. The number of intersections between diagonals and the number of interior regions increase at a super-cubic rate 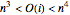 . The interior regions formed by the diagonals constitute a planar graph, but it is not the polygonization given by a Delaunay triangulation. This Demonstration presents the methods of exploiting and refining the Delaunay plane-sweep algorithm, obtaining and coloring the dual graph of a polygon mesh.
. The interior regions formed by the diagonals constitute a planar graph, but it is not the polygonization given by a Delaunay triangulation. This Demonstration presents the methods of exploiting and refining the Delaunay plane-sweep algorithm, obtaining and coloring the dual graph of a polygon mesh.
Contributed by: Stewart Dickson (February 2013)
Open content licensed under CC BY-NC-SA
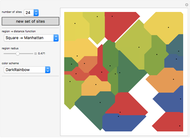
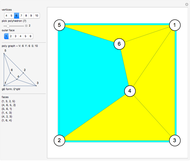
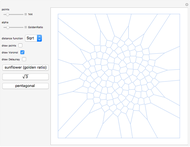
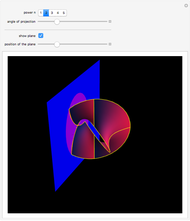
Snapshots
Details
For more information on the interior regions obtained by diagonalizing regular polygons, see [1].
A symbolic computation method generates the intersections between diagonals, and the intersections are sorted along the parameter space of the line. The code we used for this was translated from the C language [2].
We include many means for reducing the redundancy of the results we obtain at each step.
We generated a counterclockwise triangulation of the intersection points between the diagonals using ComputationalGeometry'DelaunayTriangulation. Delaunay triangulation produces unwanted triangulations of regions that should be polygons with more than three sides. We identified correct triangles and triangles to be combined into larger polygons using the originally obtained list of intersected diagonal edge segments. Triangles to be combined are a tree traversal of polygons sharing edges that are not subdivided diagonals.
Partitioning into triangles is an NP-complete problem (Wolfram MathWorld) in the theory of computation as is coloring the dual of a graph.
We apply a graph-coloring algorithm to the dual graph of the polygon mesh; exploiting the fact that the dual graph is a bipartite graph, we then apply that coloring back to the mesh.
An unexpected discovery in this Demonstration was the pattern visible in the adjacency matrix of the diagonal-diagonal intersections.
References
[1] E. S. Rowland. "Regular Polygons Project." (Feb 6, 2013) www.math.rutgers.edu/~erowland/polygons-project.html.
[2] D. Coventry. "Line-Line Intersection Algorithm." (July 11, 2008) paulbourke.net/geometry/pointlineplane/pointline.r.