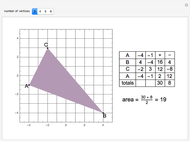
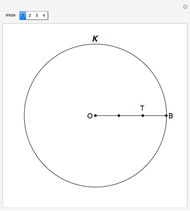
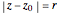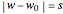Mapping Circles by a Linear Fractional Transformation
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
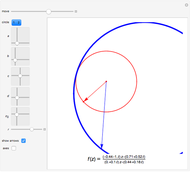
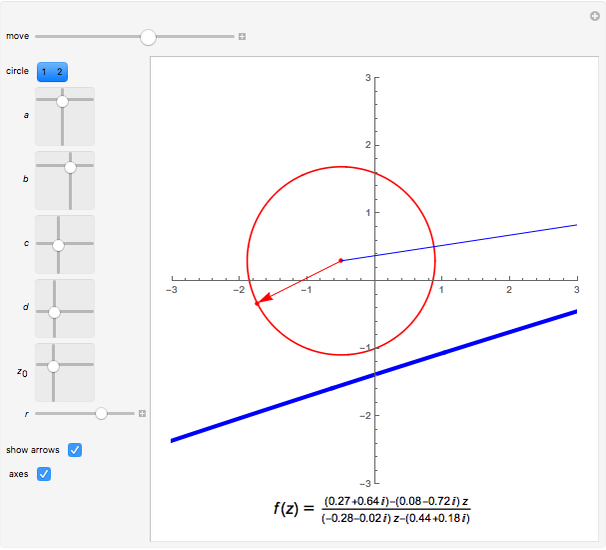
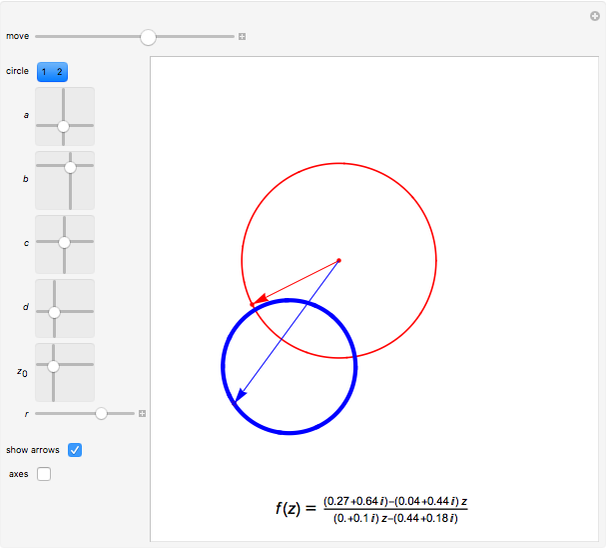
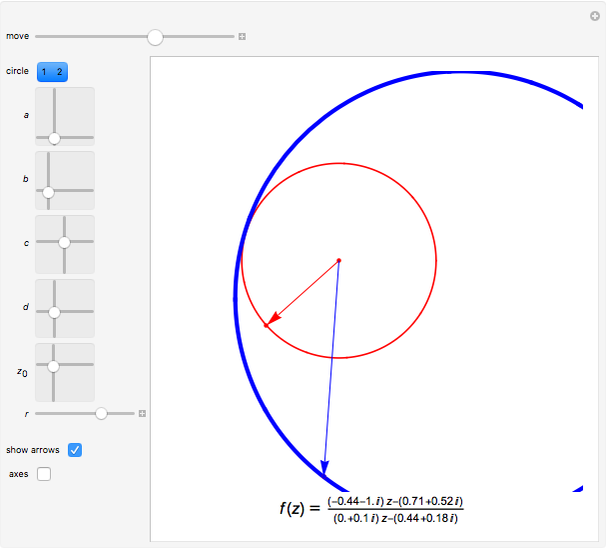
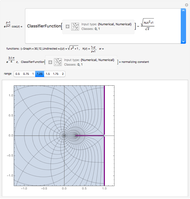
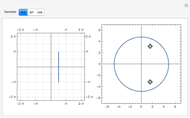
A linear fractional transformation (or Möbius transformation) in the complex plane is a conformal mapping that has the form 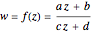 , where
, where  ,
,  ,
,  , and
, and  are complex, with
are complex, with 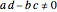 . The transformation
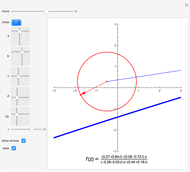
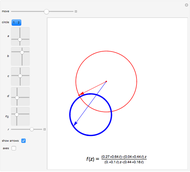
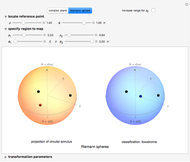
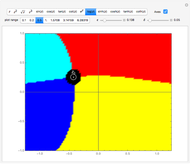
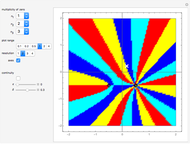
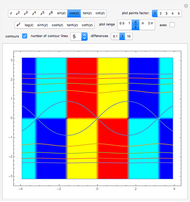
. The transformation 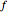 transforms circles in the
transforms circles in the  plane into circles in the
plane into circles in the 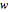 plane, where straight lines can be considered to be circles of infinite radius.
plane, where straight lines can be considered to be circles of infinite radius.
Contributed by: Izidor Hafner (February 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation