Mapping Lines and Circles onto the Riemann Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
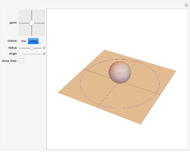
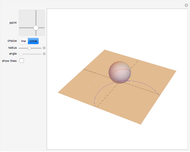
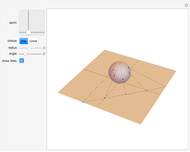
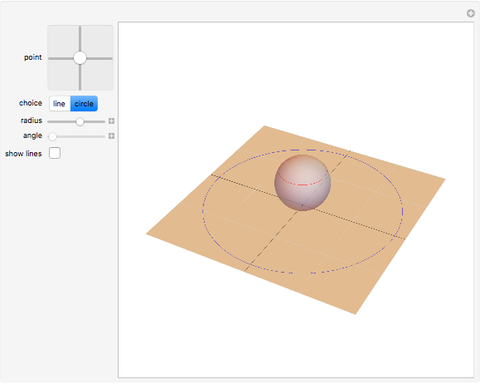
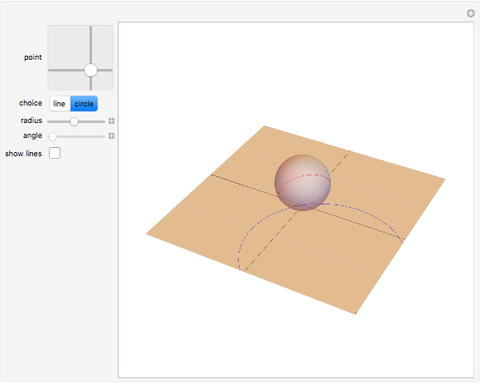
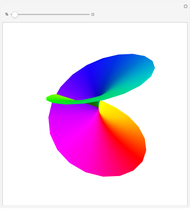
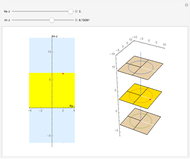
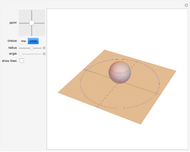
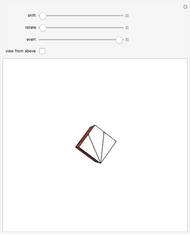
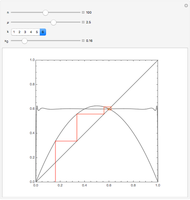
One of the great miracles of mathematics is the fact that an infinitely extended plane, which is densely packed with complex numbers, can be mapped onto a sphere with radius  and hence an area of
and hence an area of  . Here you can see a decent fraction of the complex plane and the south pole of the Riemann sphere placed at the origin.
. Here you can see a decent fraction of the complex plane and the south pole of the Riemann sphere placed at the origin.
Contributed by: Hans-Joachim Domke (July 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
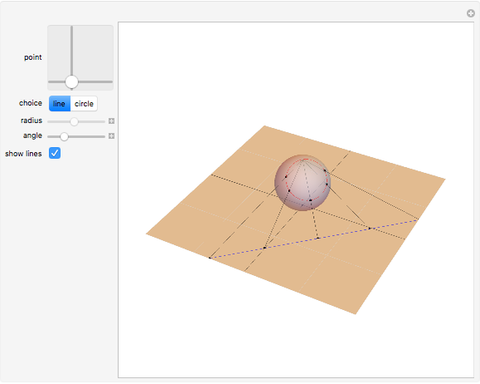
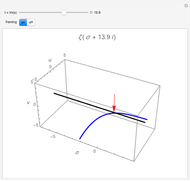
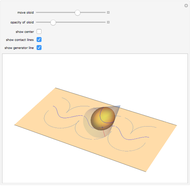
You may notice that circles with center in the origin are transformed into lines of latitude that move up to the north pole as the radius of the circle in the plane grows. Though it cannot be shown with this Demonstration, one can imagine that a circle in the plane with very large radius will be mapped onto a circle that shrinks around the north pole, while there is no point in the plane that has the north pole as an image. On the other hand, all mappings of lines contain the north pole; it is the image of the point at infinity which must be added to the plane to keep the mapping bijective. In a more descriptive way you could think of this "point" as a circle with infinite radius, but it is not part of the complex plane. One more thing that conflicts with the imagination: the interior of the unit circle in the plane is mapped onto the southern hemisphere, all other numbers outside the unit circle to the northern hemisphere.
Permanent Citation
"Mapping Lines and Circles onto the Riemann Sphere"
http://demonstrations.wolfram.com/MappingLinesAndCirclesOntoTheRiemannSphere/
Wolfram Demonstrations Project
Published: July 13 2009