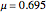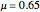Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Mapping the Maxima for a Nonisothermal Chemical System

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

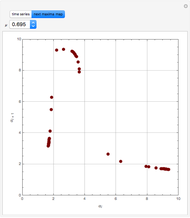
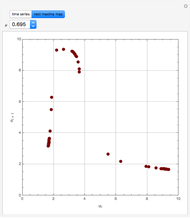
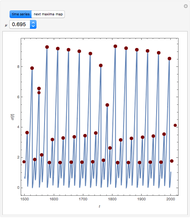
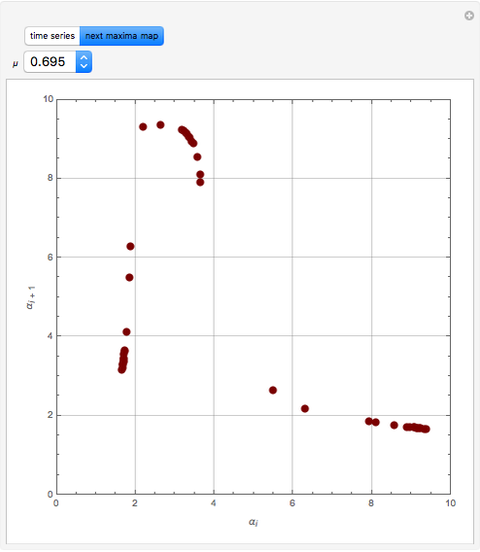
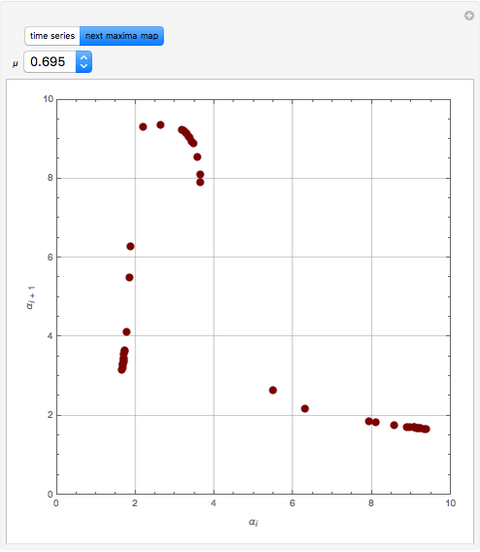
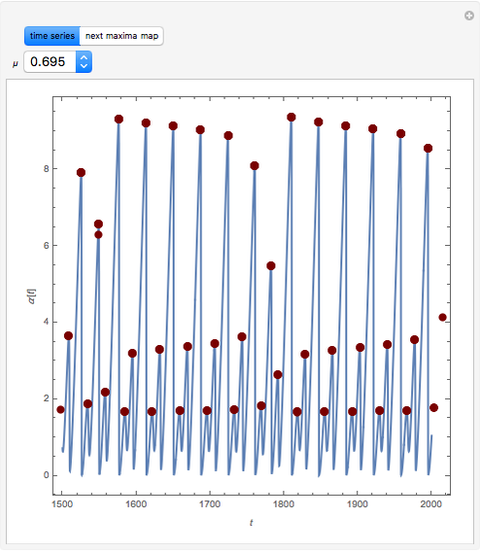
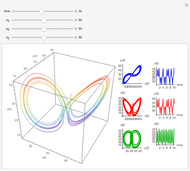
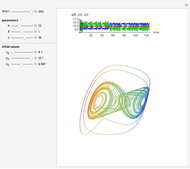
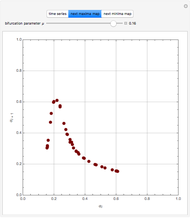
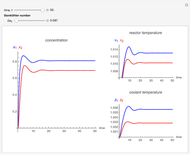
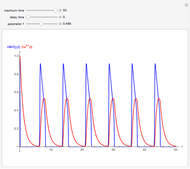
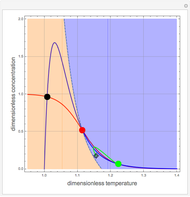
Scott and Tomlin derived three coupled nonlinear ODEs to describe the behavior of a nonisothermal chemical system [1].

[more]

This Demonstration plots the loci of the maxima of the time series and uses this information to map the next maximum point.

For particular values of the bifurcation parameter (for example, ), the result is chemical chaos, and a map of the next maximum shows the typical behavior of a chaotic attractor.

On the other hand, when periodic behavior is observed (e.g., for ), a map of the next maximum displays only a small number of isolated points.

[less]

Contributed by: Housam Binous (August 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

[1] S. K. Scott and A. S. Tomlin, "Period Doubling and Other Complex Bifurcations in Non-Isothermal Chemical Systems," Philosophical Transactions of the Royal Society A, 332(1624), 1990 pp. 51–68. rsta.royalsocietypublishing.org/content/332/1624/51.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send