Matrix Representation of the Permutation Group

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
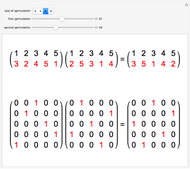
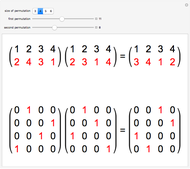
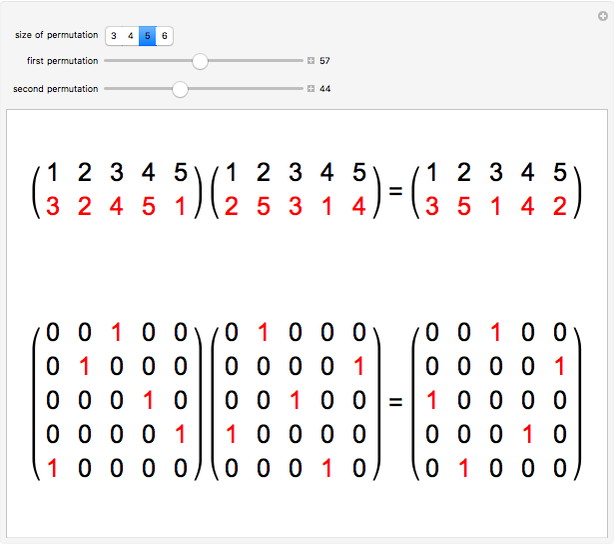
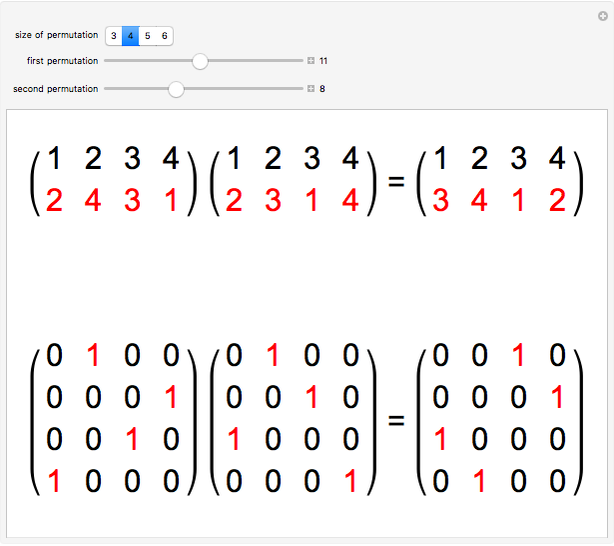
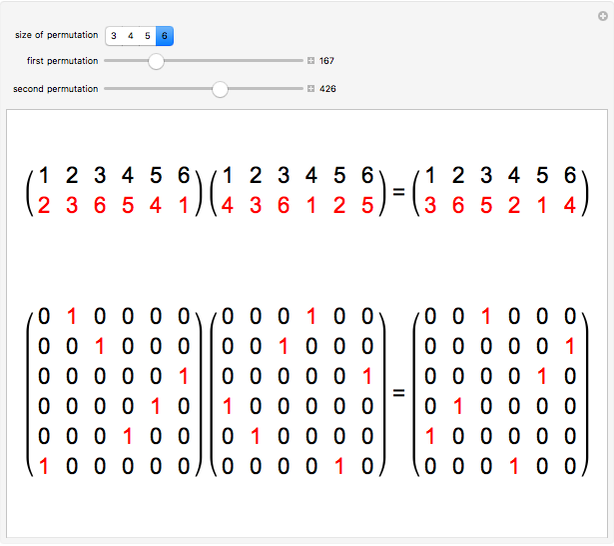
The set  of all permutations of
of all permutations of  forms a group under the multiplication (composition) of permutations; that is, it meets the requirements of closure, existence of identity and inverses, and associativity. We can set up a bijection between
forms a group under the multiplication (composition) of permutations; that is, it meets the requirements of closure, existence of identity and inverses, and associativity. We can set up a bijection between  and a set of binary
and a set of binary  matrices (the permutation matrices) that preserves this structure under the operation of matrix multiplication. The bijection associates the permutation
matrices (the permutation matrices) that preserves this structure under the operation of matrix multiplication. The bijection associates the permutation  with the matrix
with the matrix  , with zeros everywhere except for ones at row
, with zeros everywhere except for ones at row , column
, column  , for
, for  .
.
Contributed by: Jaime Rangel-Mondragon (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Matrix Representation of the Permutation Group"
http://demonstrations.wolfram.com/MatrixRepresentationOfThePermutationGroup/
Wolfram Demonstrations Project
Published: August 2 2012