Maximize the Number of Vertices in an Equilateral Triangular Lattice

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
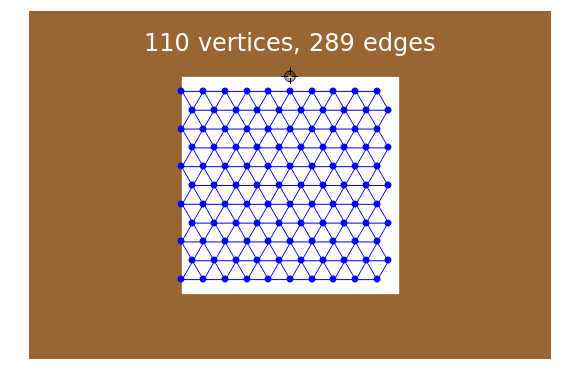
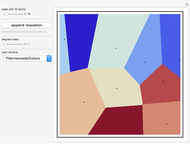
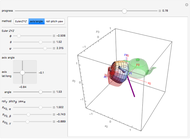
An equilateral triangular lattice is parameterized by four variables: an  and
and  offset for the initial vertex, the angle
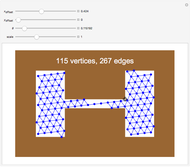
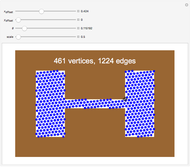
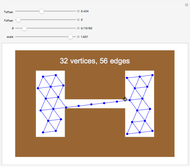
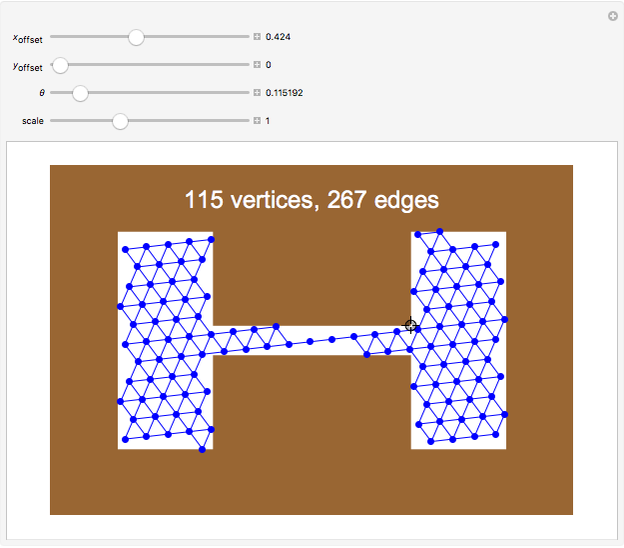
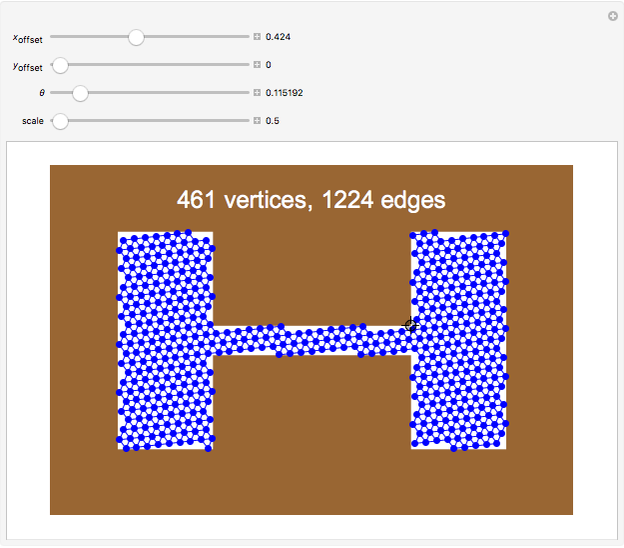
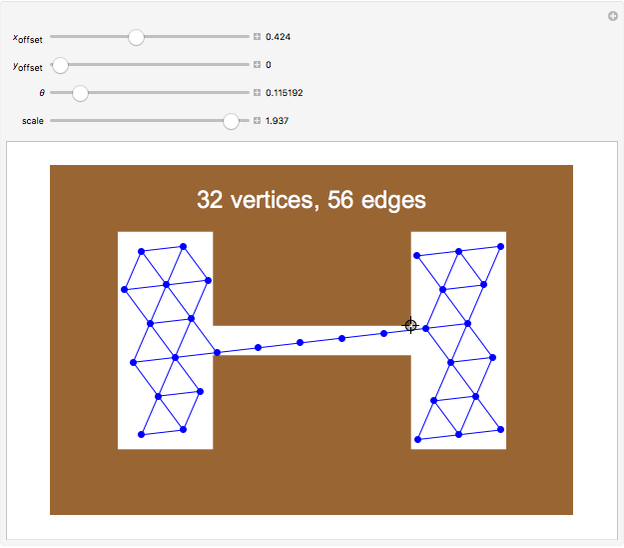
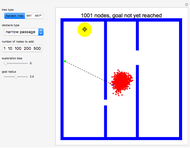
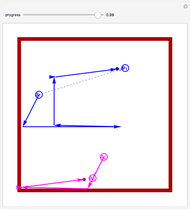
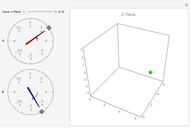
offset for the initial vertex, the angle  of the grid with respect to the horizontal, and a scale parameter for the edge lengths. In this Demonstration, you can vary these parameters and see how many vertices and edges fit in the open workspace (white). Drag the locator to create a "narrow passage," while keeping the area of the workspace constant.
of the grid with respect to the horizontal, and a scale parameter for the edge lengths. In this Demonstration, you can vary these parameters and see how many vertices and edges fit in the open workspace (white). Drag the locator to create a "narrow passage," while keeping the area of the workspace constant.
Contributed by: Aaron T. Becker (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let 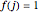 if
if  is even, and 0 otherwise. The positions of the vertices in an equilateral triangular lattice indexed by
is even, and 0 otherwise. The positions of the vertices in an equilateral triangular lattice indexed by 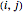 are
are  .
.
These positions can be modified by a scale parameter 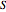 , a rotation
, a rotation  , and the offset
, and the offset  :
:
 .
.
Narrow passages are an important concept in motion planning. A narrow passage is a small region whose removal changes the connectivity of the configuration space.
Permanent Citation