Maximizing Apparent Velocity in a Camera's Frame

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
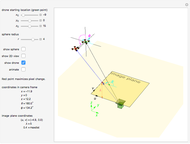
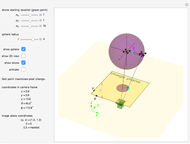
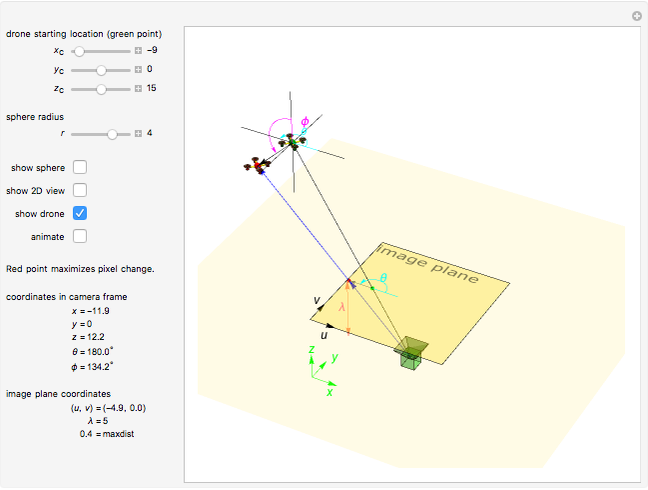
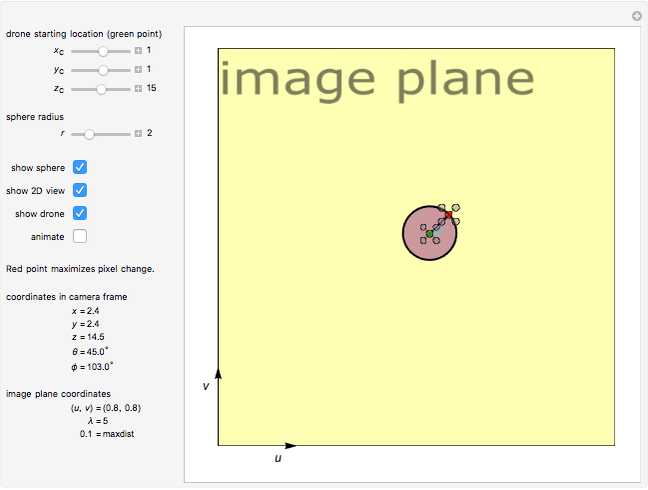
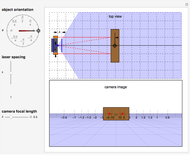
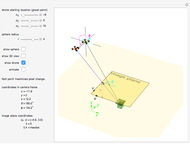
How should a drone move to maximize its apparent velocity in the frame of a camera? This Demonstration solves this problem for a drone that can move a distance  in any direction.
in any direction.
Contributed by: Mohammad Sultan and Aaron T. Becker (November 2018)
Open content licensed under CC BY-NC-SA
Details
If a drone (represented as a particle) can move with equal velocity in any direction, the set of possible 3D coordinates after one time step is a 3D sphere. The image plane of a camera projects all 3D points into a 2D camera frame [1]. If the sphere is centered at  with radius
with radius  and camera focal length
and camera focal length 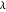 , then the optimal goal location
, then the optimal goal location  for the drone is parameterized by the (latitude, longitude) pair
for the drone is parameterized by the (latitude, longitude) pair 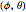 :
:
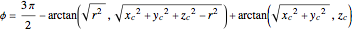 ,
,
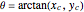 .
.
If 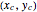 is
is 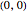 , there are infinite solutions with
, there are infinite solutions with 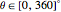 .
.
The goal location is:

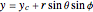

This projects onto the image plane at the point 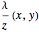 . Because
. Because 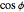 is always negative, the drone decreases the distance in
is always negative, the drone decreases the distance in  . Interestingly, the sphere projects into a 2D ellipse in the image plane. With equations given by [2], the ellipse is centered at
. Interestingly, the sphere projects into a 2D ellipse in the image plane. With equations given by [2], the ellipse is centered at
 ,
,
with
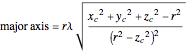 ,
,
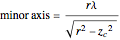
and
 .
.
The focal length 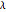 is 5 in this Demonstration.
is 5 in this Demonstration.
Snapshot 1:  ,
, 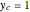 ,
,  and
and 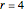
Snapshot 2: 2D view when 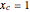 ,
, 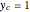 ,
,  and
and 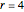
Snapshot 3: 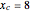 ,
,  ,
,  and
and 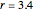 with "show drone" turned off
with "show drone" turned off
Snapshot 4: 2D view when  ,
, 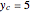 ,
,  and
and 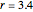 with "show sphere" turned off
with "show sphere" turned off
Snapshot 5: 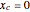 ,
, 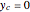 ,
,  and
and 
Snapshot 6: 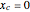 ,
, 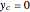 ,
,  and
and  with "show drone" turned off
with "show drone" turned off
Snapshot 7: 2D view when 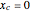 ,
, 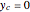 ,
,  and
and 
References
[1] M. W. Spong, S. Hutchinson and M. Vidyasagar, Robot Modeling and Control, Hoboken, NJ: John Wiley and Sons, 2006.
[2] D. Eberly. "Perspective Projection of an Ellipsoid." (Oct 30, 2018) www.geometrictools.com/Documentation/PerspectiveProjectionEllipsoid.pdf.
Snapshots
Permanent Citation