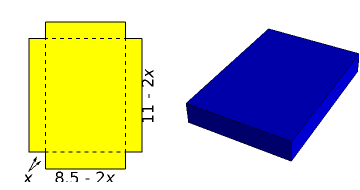
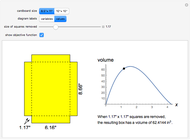
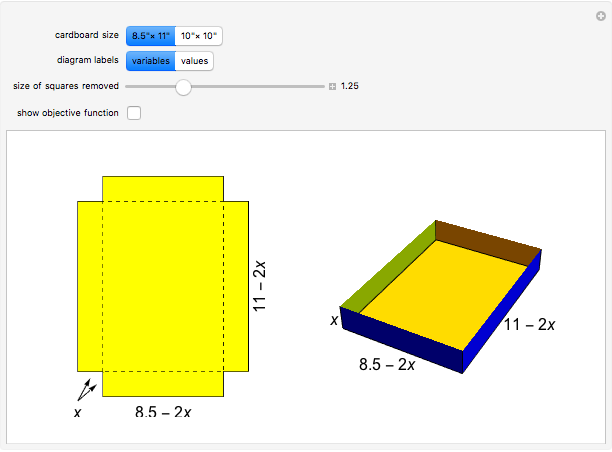
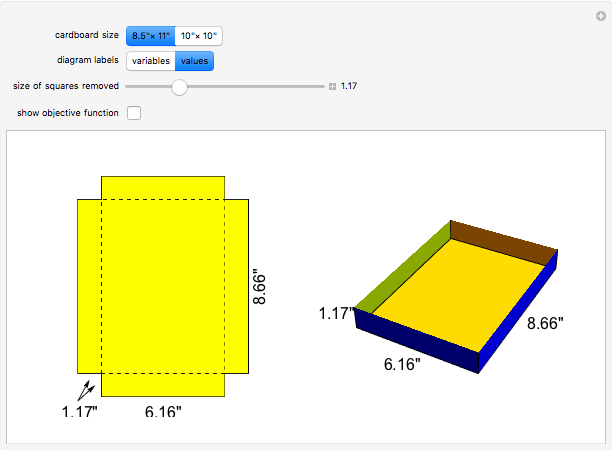
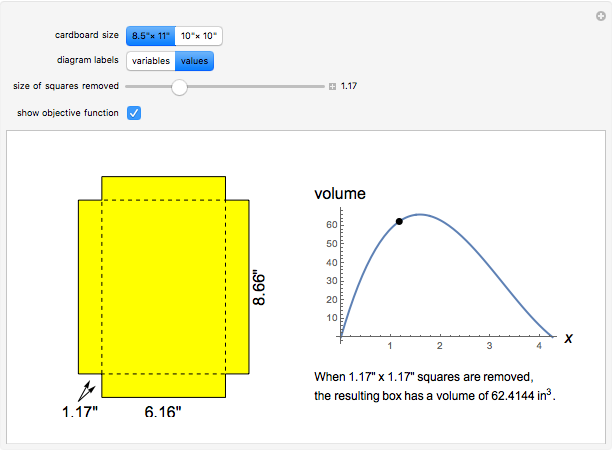
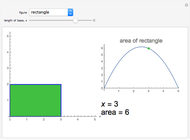
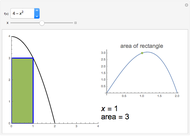
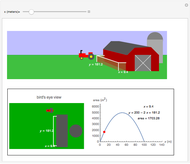
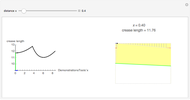
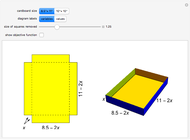
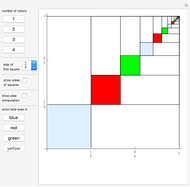
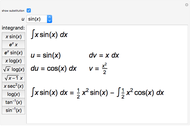
A standard problem in a first-semester calculus course is to maximize the volume of a box made by removing squares of equal size from the corners of a rectangular piece of cardboard and folding the remaining pieces. This Demonstration lets you see the relationship between the size of the squares removed and the shape and volume of the resulting box. Two sizes of cardboard sheets are available, and the diagrams can be labeled with either a symbolic variable or numerical values.