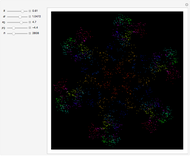
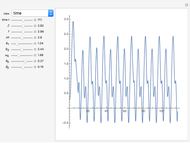
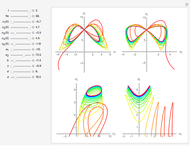
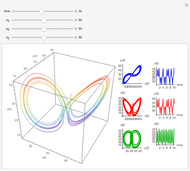
In nonlinear optics, the Maxwell–Bloch equations can be used to describe laser systems. They consist of three first-order equations for the electric field in a single longitudinal cavity mode, which became nonlinear because the system oscillates between at least two discrete energy levels. The system is derived from Maxwell's equations, using semiclassical approximations for quantum variables. The equations are solved for population inversion density and mean atomic-polarization density , induced by an electric field . Here is the decay rate in the laser cavity due to beam transmission. 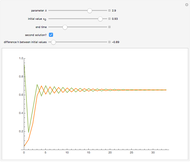The parameters and are decay rates of atomic polarization and population inversion and is a pumping energy parameter. Chaotic behavior and period doubling has been observed experimentally. These equations are related to the Lorenz equations and can exhibit strange attractors.