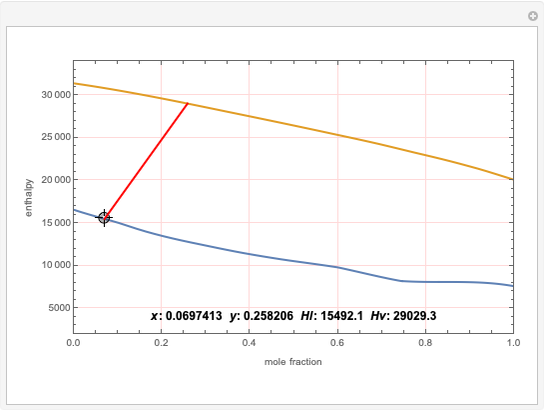
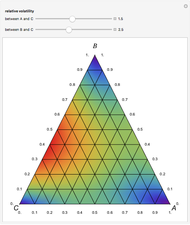
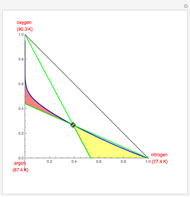
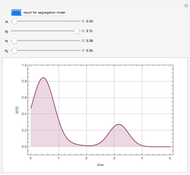
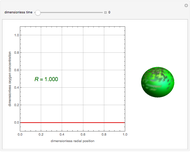
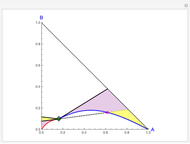
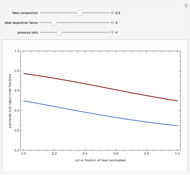
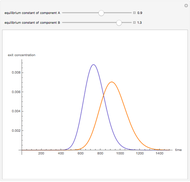
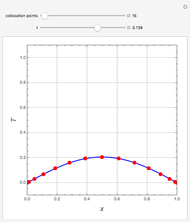
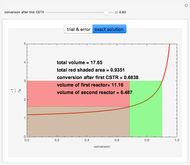
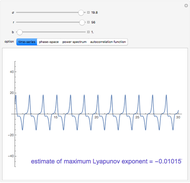
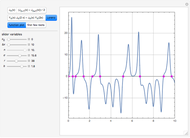
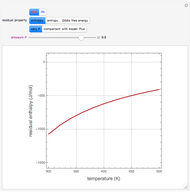
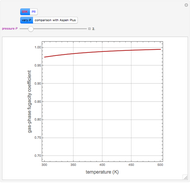
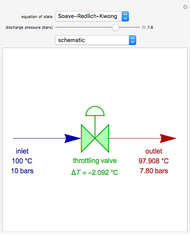
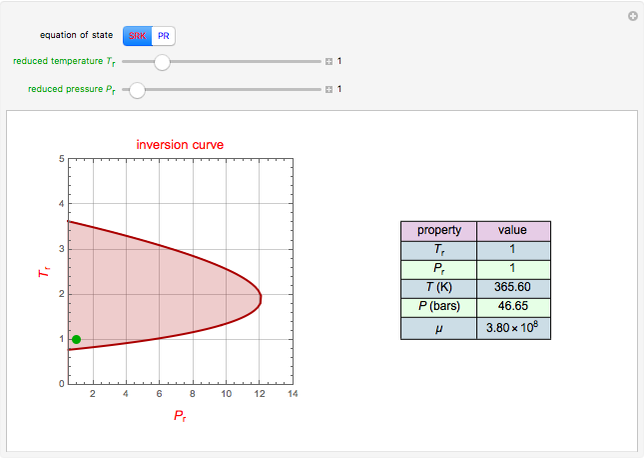
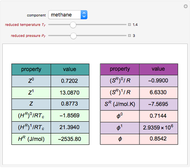
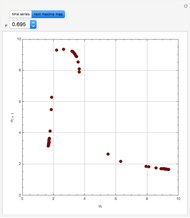
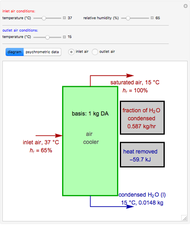
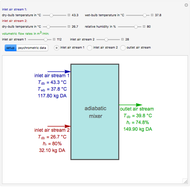
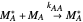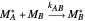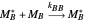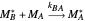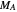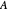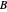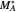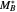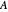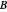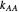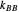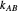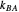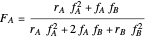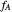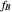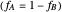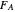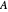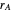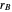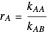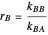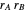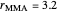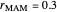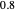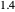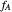Copolymer composition is a significant parameter in determining the properties of the copolymer, and ultimately, its practical applications. To predict copolymer composition during the polymerization process, one has to determine the concentrations of the monomers in the reactor and their reactivities.
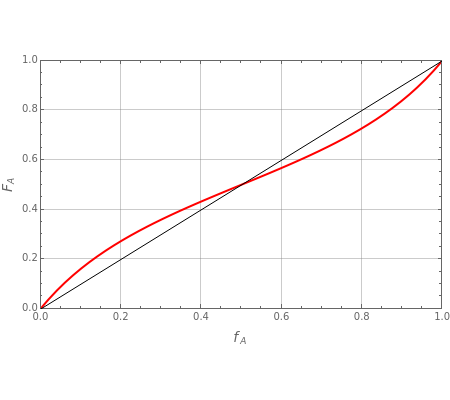
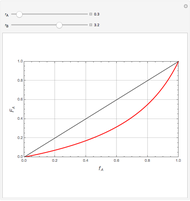
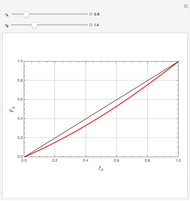
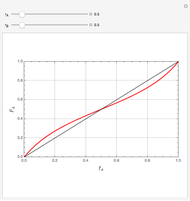
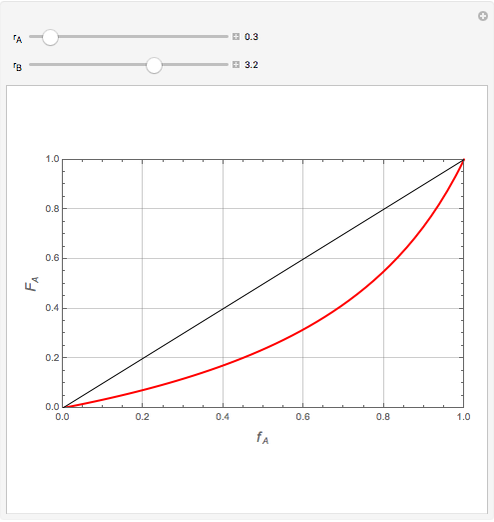
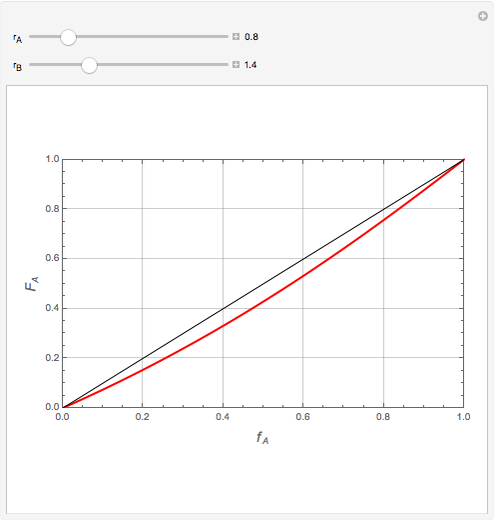
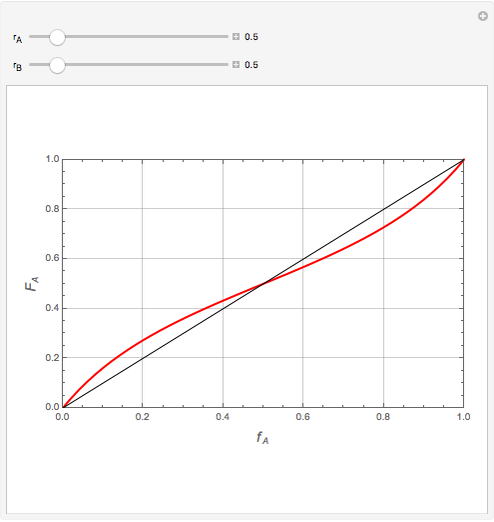
Mayo and Lewis [1] developed a simple equation to measure the instantaneous copolymer composition as a function of both the feed composition and the monomers' reactivity ratios. This model is based on the following four possible propagation reactions:
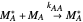 ,
,
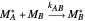 ,
,
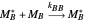 ,
,
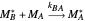 ,
,
where 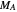 and
and  are the monomers
are the monomers 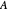 and
and 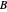 , respectively,
, respectively, 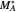 and
and 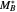 are growing chains terminating with
are growing chains terminating with 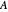 and
and 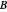 units, respectively, and
units, respectively, and 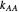 ,
, 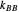 ,
, 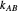 , and
, and 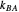 are propagation rate constants.
are propagation rate constants.
The final expression for the Mayo–Lewis equation is:
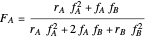 ,
,
where 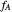 and
and 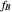 are the mole fractions of the monomers in the feed
are the mole fractions of the monomers in the feed 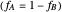 ,
, 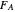 is the mole fraction of
is the mole fraction of 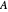 formed in the copolymer, and
formed in the copolymer, and 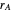 and
and 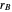 are the reactivity ratios given by:
are the reactivity ratios given by: 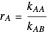 and
and 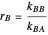 .
.
The copolymer structures can be predicted by knowing the absolute values of the reactivity ratios. For example:
1. If 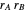 is close to 1, then the resultant copolymer has an ideal random structure. The copolymerization of methyl methacrylate and methacrylamide is a clear example of such a system (
is close to 1, then the resultant copolymer has an ideal random structure. The copolymerization of methyl methacrylate and methacrylamide is a clear example of such a system (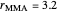 and
and 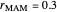 ). Most of the copolymers are in this category and thus have the tendency to be random. Styrene, with a reactivity ratio of
). Most of the copolymers are in this category and thus have the tendency to be random. Styrene, with a reactivity ratio of 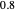 , and butadiene, with a reactivity ratio of
, and butadiene, with a reactivity ratio of 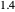 , are other examples of random copolymers.
, are other examples of random copolymers.
2. If at least one of the reactivity ratios is equal to zero, then the resulting copolymer has an alternating structure. For example, for the copolymerization involving a two-component system composed of styrene and maleic anhydride, both reactivity ratios are equal to zero.
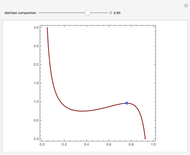
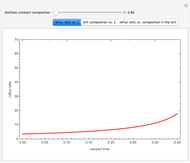
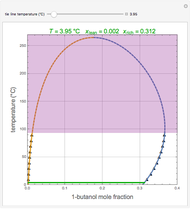
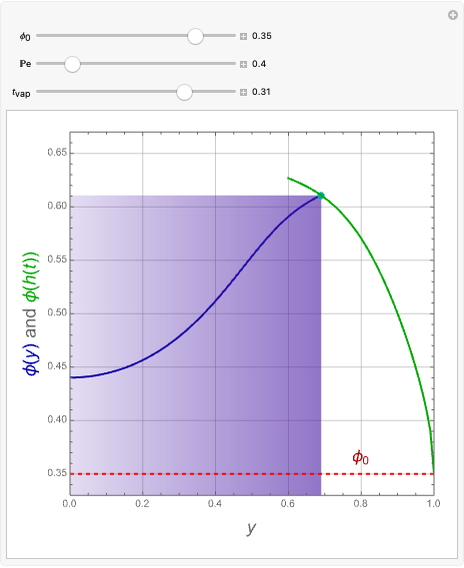
Similarly to a bicomponent liquid mixture, azeotropic compositions exist in some copolymerization processes. This azeotropic composition leads to a composition drift in the final product. If both reactivity ratios are equal to one, then all the values of 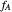 in the Mayo–Lewis equation have azeotropic composition. For more information about the subject, the reader can consult the excellent textbook by Rudin [2].
in the Mayo–Lewis equation have azeotropic composition. For more information about the subject, the reader can consult the excellent textbook by Rudin [2].
[less]

 , 1944 pp. 1594–1601. doi:10.1021/ja01237a052.
, 1944 pp. 1594–1601. doi:10.1021/ja01237a052.