McCabe-Thiele Method for Methanol/Water Separation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
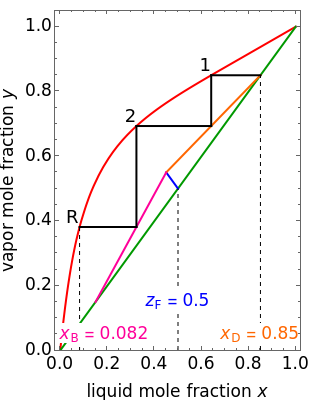
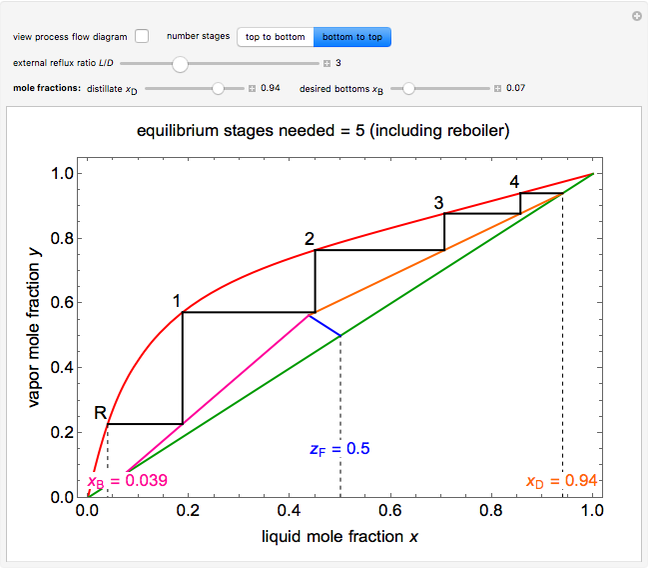
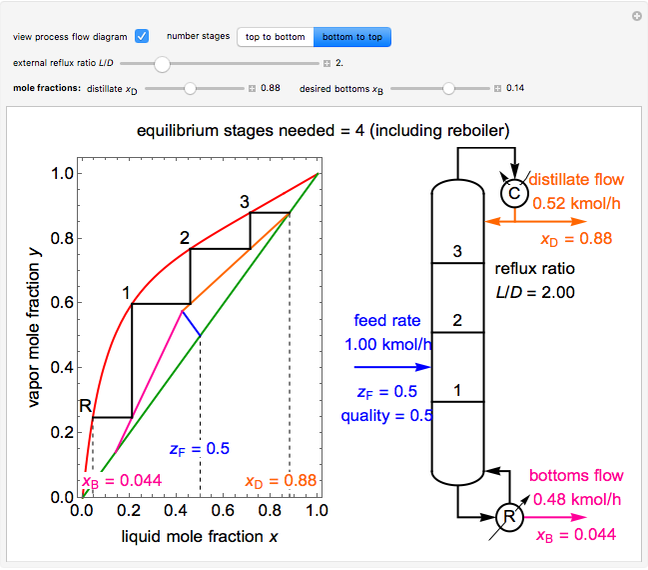
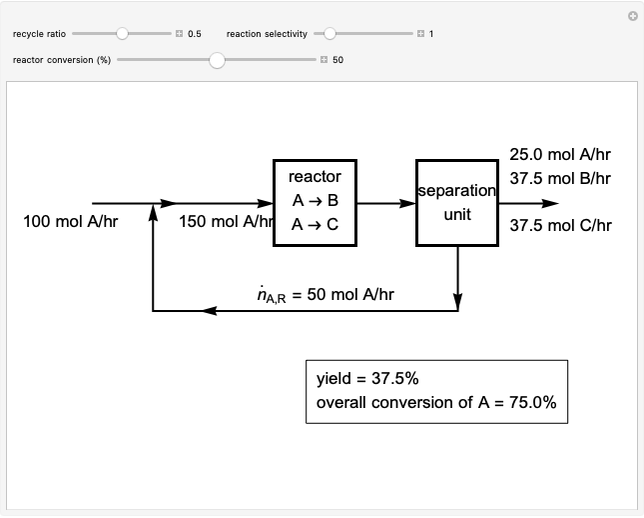
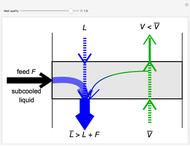
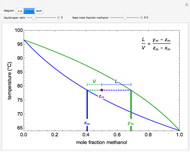
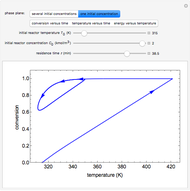
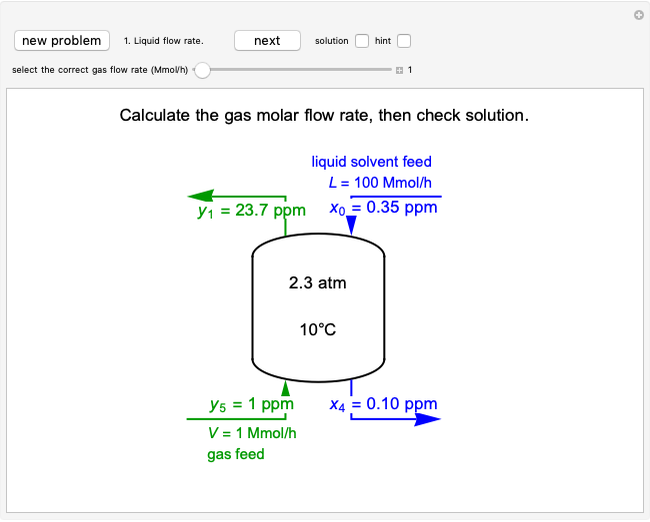
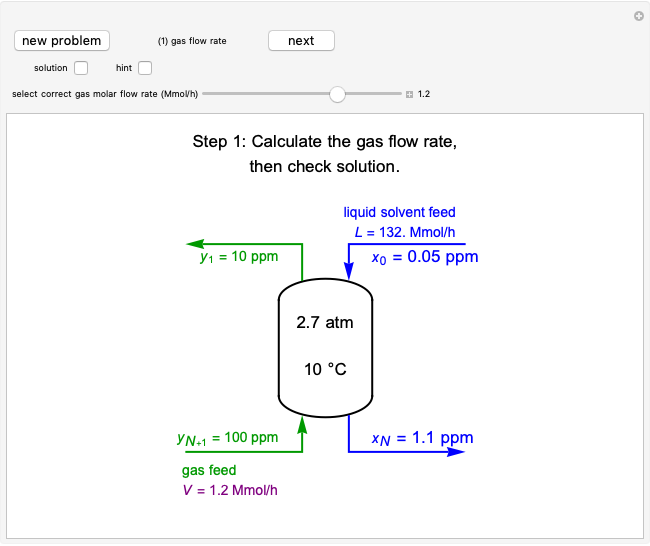
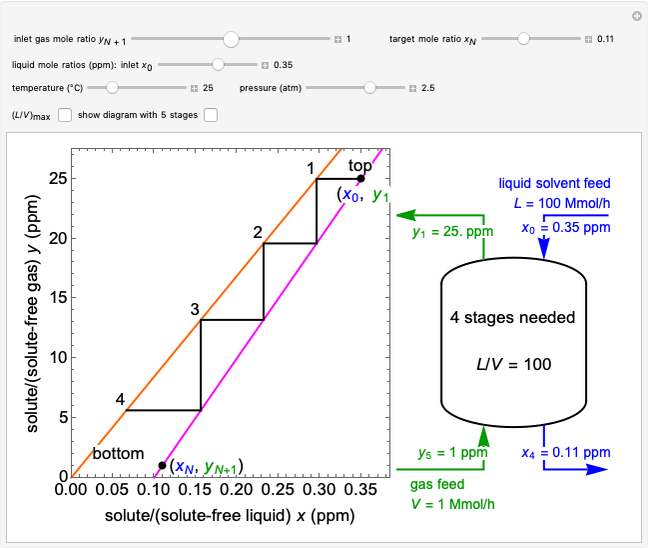
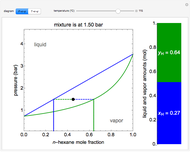
This Demonstration shows how to determine the number of equilibrium stages needed for a two-component (methanol/water) separation in a counter-current distillation column. It also shows the optimal location to feed the binary mixture into the column. Check "view process flow diagram" to show the 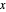 -
-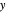 diagram on the left and the process flow diagram on the right. When that box is not checked, a larger
diagram on the left and the process flow diagram on the right. When that box is not checked, a larger 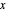 -
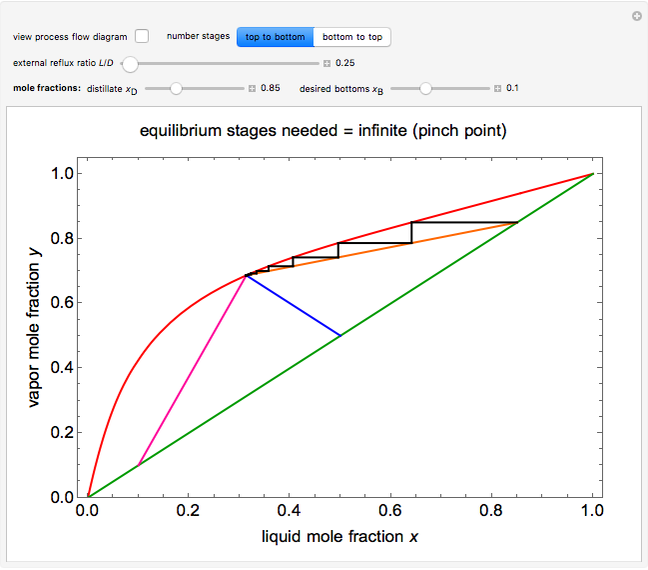
-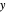 diagram is shown and you can move the cursor over the curves to see labels. The column feed has a methanol mole fraction of
diagram is shown and you can move the cursor over the curves to see labels. The column feed has a methanol mole fraction of 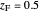 and a quality of 0.5. The condenser is a total condenser, so it is not considered an equilibrium stage. Set the external reflux ratio
and a quality of 0.5. The condenser is a total condenser, so it is not considered an equilibrium stage. Set the external reflux ratio 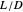 , as well as the methanol mole fractions in the distillate
, as well as the methanol mole fractions in the distillate  and bottoms
and bottoms 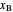 streams, with sliders. The number of stages is determined by stepping off stages starting at
streams, with sliders. The number of stages is determined by stepping off stages starting at 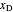 ; the partial reboiler is an equilibrium stage. The number of equilibrium stages depends on the compositions of the exiting streams and the reflux ratio. The stages can be numbered with the first stage above the reboiler (bottom to top) or with the first stage at the condenser, use buttons to switch between these numbering options. Note that the
; the partial reboiler is an equilibrium stage. The number of equilibrium stages depends on the compositions of the exiting streams and the reflux ratio. The stages can be numbered with the first stage above the reboiler (bottom to top) or with the first stage at the condenser, use buttons to switch between these numbering options. Note that the 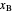 determined by stepping off stages is often lower than the desired
determined by stepping off stages is often lower than the desired 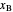 because reaching the exact value of the desired
because reaching the exact value of the desired 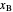 would require a partial stage, which is not possible.
would require a partial stage, which is not possible.
Contributed by: Neil Hendren and Rachael L. Baumann (October 2016)
Additional contributions by: John L. Falconer and Thomas Belval
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The McCabe–Thiele graphical solution method for binary distillation is used to determine the number of equilibrium stages needed to achieve a specified separation in a distillation column. This method assumes:
1. The distillation column is adiabatic.
2. Constant molar overflow (CMO), which means that for every mole of vapor condensed, one mole of liquid is vaporized. This results in constant liquid and vapor flow rates between stages (the exception being the flow rates of the stages above and below the feed stream, which are not equal). This assumption requires that:
2a. Specific heat changes are small compared to latent heat changes between stages 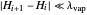 and
and 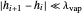 .
.
2b. Heat of vaporization 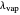 is the same for both components and thus independent of concentration.
is the same for both components and thus independent of concentration.
3. Heat of mixing is negligible.
The equilibrium curve was calculated using the modified Raoult's law:
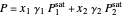 ,
,
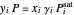 ,
,
where 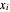 and
and 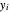 are the liquid and vapor mole fractions (
are the liquid and vapor mole fractions (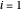 for methanol,
for methanol, 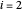 for water),
for water), 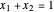 ,
, 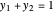 ,
, 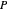 is total pressure and
is total pressure and 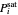 is the saturation pressure, which is calculated using the Antoine equation:
is the saturation pressure, which is calculated using the Antoine equation:
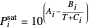 ,
,
where 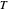 is temperature, and
is temperature, and 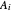 ,
, 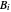 and
and 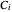 are Antoine constants.
are Antoine constants.
The activity coefficients 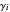 are calculated using the two-parameter Margules model:
are calculated using the two-parameter Margules model:
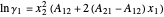 ,
,
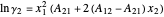 ,
,
where 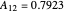 and
and 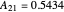 are the Margules parameters for a methanol/water mixture.
are the Margules parameters for a methanol/water mixture.
The operating lines for the rectifying and stripping sections are used to determine the number of stages. First the feed and rectifying operating lines are calculated:
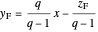 ,
,
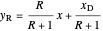 ,
,
where  is the vapor quality of the feed,
is the vapor quality of the feed, 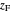 is the mole fraction of methanol in the feed,
is the mole fraction of methanol in the feed, 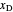 is the liquid mole fraction of methanol in the distillate and
is the liquid mole fraction of methanol in the distillate and 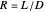 is the reflux ratio.
is the reflux ratio.
The operating line for the stripping section 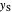 is found by drawing a line through the bottoms composition
is found by drawing a line through the bottoms composition 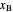 on the
on the 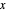 –
–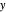 line and the intersection of the feed line (also called the
line and the intersection of the feed line (also called the  line)
line) 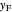 and rectifying line
and rectifying line 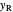 . The feed line intersects the rectifying line at
. The feed line intersects the rectifying line at 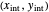 :
:
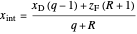 ,
,
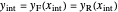 ,
,
the slope of the stripping line is calculated from 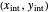 and
and 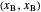 and the
and the  intercept is found:
intercept is found:
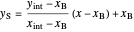 .
.
View the screencast videos at [1] and [2] for a step-by-step explanation of the McCabe–Thiele method.
References
[1] McCabe–Thiele Graphical Method Example Part 1 [Video]. (Mar 6, 2014) www.youtube.com/watch?v=Cv4KjY2BJTA.
[2] McCabe-Thiele Graphical Method Example Part 2 [Video]. (Mar 6, 2014) www.youtube.com/watch?v=eIJk5uXmBRc.
Permanent Citation