Mechanism of a Solar Cell

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
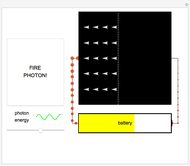
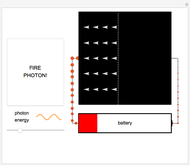
Fire photons with selected energies into the solar cell. Photons with enough energy can excite electrons into a higher state. Subsequently, the electrons diffuse randomly throughout the cell. If they cross a certain threshold, they fall downhill (energetically), and power the battery.
Contributed by: Christopher P. Muzzillo (July 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
How is a solar cell powered? Sometimes turning the problem upside down can be fun and more revealing. So it might be more informative to ask another question, how are solar cells not powered? Or, why can the very best solar cell still "only" convert around 46% of the Sun's power into usable power? This Demonstration illustrates answers to these questions and more.
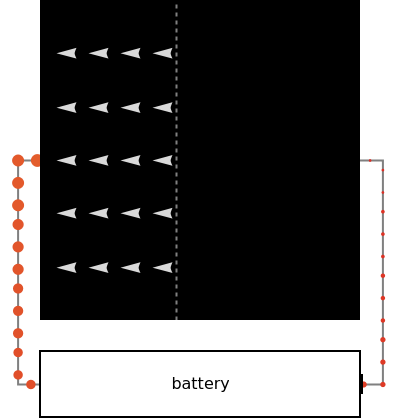
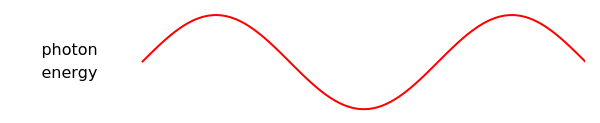
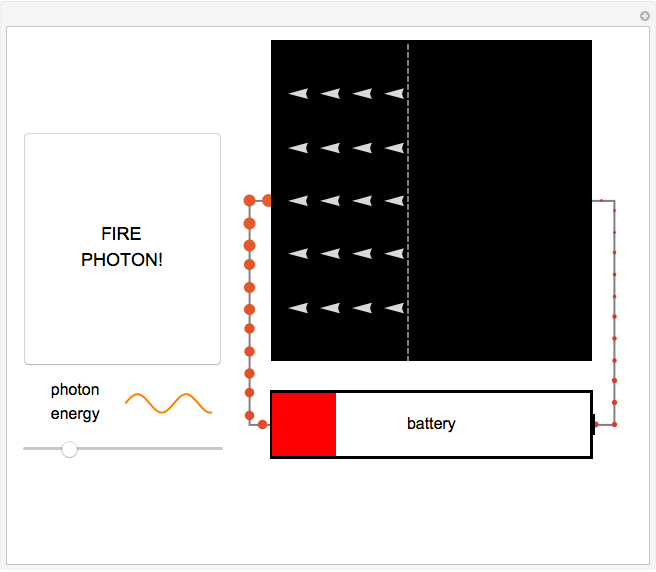
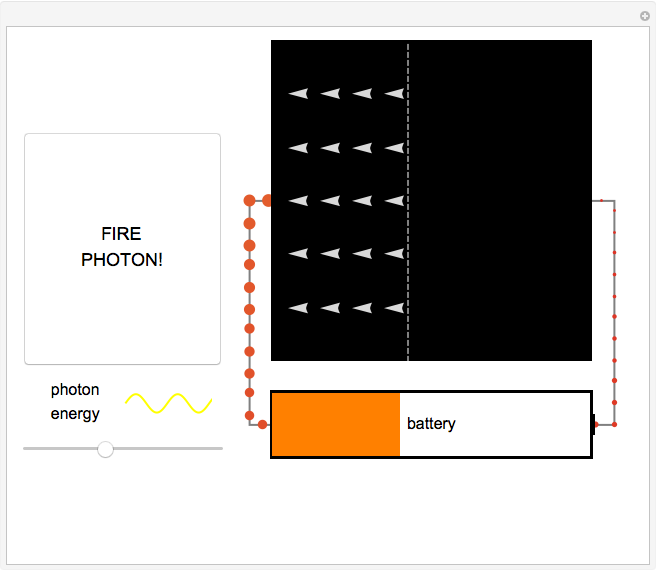
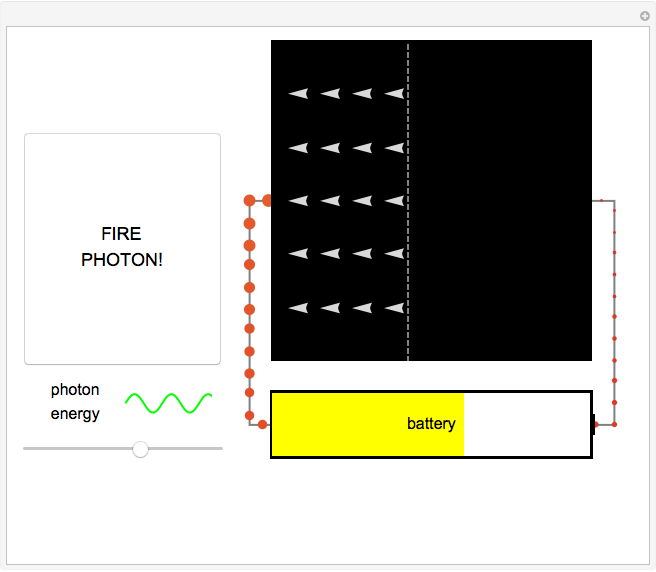
In this Demonstration, photon energy determines wavelength and color. Electrons are shown as circles with different sizes and colors, depending on their energies. Small electrons and long wavelength photons are red and low energy. Large electrons and short wavelength photons are purple and high energy.
Click the button "FIRE PHOTON!" When you fire a photon of a chosen energy into the device, it may or may not be absorbed, depending on its energy. If the photon has too little energy, it simply passes through the device. However, if the photon has energy above a certain threshold, it is absorbed, transferring its energy to an electron. When this occurs, the electron is excited to a continuous band of energy states, which is spread out spatially. The electron can remain in the higher-energy band of states for a relatively long time. In the Demonstration, try to figure out which colored photons do not have enough energy to excite the electron to this band. This energy limits solar cell performance.
Now, if a photon has a lot more energy than the gap between bands of electron states, then the excess energy is wasted. The most favorable course for these highly excited electrons is to quickly relax (to the band edge), much like the way a baseball thrown straight up tends to fall back down to the ground. This means that very soon after being excited by the photon, the electrons release energy to their surroundings (by collisions with another electron or a nucleus, emitting a photon, etc.). In the Demonstration, try to find which photon energies excite the electrons too highly so that a large fraction of the energy is lost. This also reduces energy conversion efficiency.
Once an electron is excited to this new, higher-energy band of states, it becomes free to randomly wander around in space. Because these electrons are no longer confined, they are called conducting electrons. But the solar cell is built in a clever way: like a trap. If the conducting electrons happen to randomly wander across the threshold of the trap, then it is favorable for them to start falling down an energetic hill (toward the left).
In the Demonstration, try to find where this hill is located and where it leads the conducting electrons to as they fall. Much like water at the source of a river forces flow at the river's end, this action of falling downhill also causes electron drift everywhere else around the circuit. For this to occur, the electrons must lose some energy throughout their entire journey, much like rivers flowing only downhill. This is another reason not all of the light's energy can be converted into usable power. Since this entire chain of events was initiated by incoming photons, energy is input to the circuit, charging the battery. Note that the electrons lose the largest amount of energy/size/color to the battery, so the solar cell is indeed doing its job. Can you think of ways to increase the amount of energy transferred to the battery? Then try to figure out how to make them work and solve the world's energy problems!
Notes
Nothing is to scale.
The black box is a 2D representation of the solar cell's innards. Electrons are moving around in two dimensions instead of the real 3D situation.
Lower-energy photons must travel further into the device to be absorbed.
Photons with energies below the band gap pass through without being absorbed.
Conducting electrons are always wandering around at random; this is diffusion and dominates on the right side.
Conducting electrons fall downhill or drift down a potential energy gradient, on the left side.
Diffusion occurs in the left part too (not in the Demonstration) but is dominated by drift.
Electrons can "disappear" or recombine on the left side (not in the Demonstration).
Electrons in the circuit lose a small amount of energy; this is resistance.
Electrons reenter the device on the other side with about as much energy as they had before photon absorption. If the circuit were not completed there, all the electrons would stop drifting. This is exactly what occurs when the battery is fully charged (the potential energy gradient forcing electrons to drift disappears).
An advanced topic concerns the holes that electrons leave behind in the localized valence band, which are incredibly useful entities, both conceptually and mathematically.
Permanent Citation
"Mechanism of a Solar Cell"
http://demonstrations.wolfram.com/MechanismOfASolarCell/
Wolfram Demonstrations Project
Published: July 17 2015