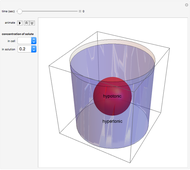
Membrane Concentration Profile

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
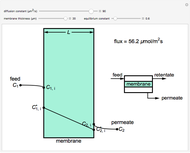
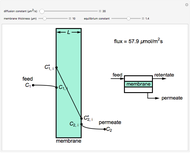
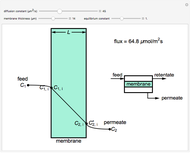
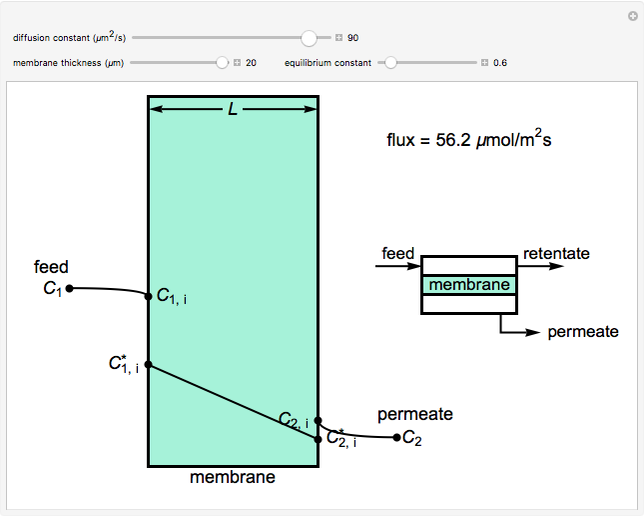
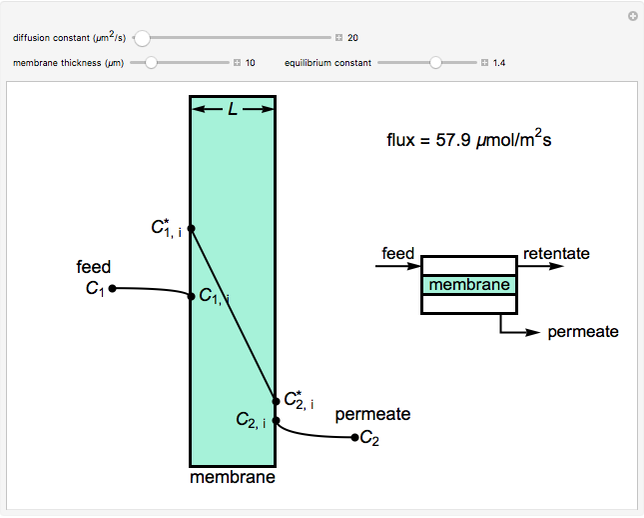
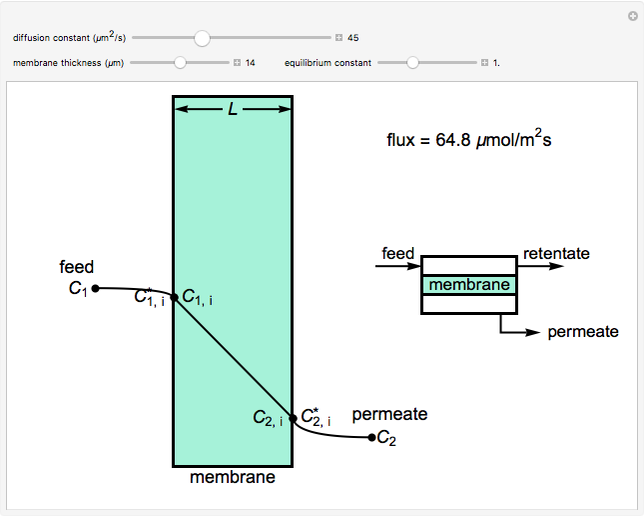
This Demonstration shows the concentration profiles on the feed and permeate sides of a membrane resulting from a diffusion boundary layer and the concentration profile inside the membrane. It also calculates the molar flux through the membrane. Use the sliders to change the membrane diffusion constant, the equilibrium constant and the membrane thickness. The feed concentration  and the desired permeate concentration
and the desired permeate concentration 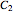 are set. Place your cursor over a black dot to see its concentration displayed on the right.
are set. Place your cursor over a black dot to see its concentration displayed on the right.
Contributed by: Rachael L. Baumann (March 2017)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The molar flux at steady state is calculated using the analog of series resistances. The flux through each layer is:
feed:
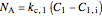 ,
,
membrane:
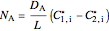 ,
,
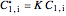 ,
,
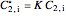 ,
,
permeate:
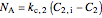 ,
,
where  is the mass transfer coefficient,
is the mass transfer coefficient,  and
and 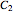 are the feed and permeate concentrations,
are the feed and permeate concentrations, 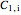 and
and  are the concentrations at the interface,
are the concentrations at the interface, 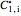 and
and  are the concentrations at the surfaces,
are the concentrations at the surfaces, 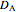 is diffusivity in the membrane,
is diffusivity in the membrane, 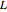 is membrane thickness and
is membrane thickness and 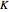 is the equilibrium constant.
is the equilibrium constant.
The flux through the membrane can be written in terms of permeance  :
:
 ,
,
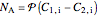 .
.
Because the system is at steady state, 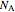 is the same through all three layers:
is the same through all three layers:
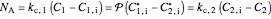 .
.
Solving each 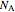 equation for the concentration differences:
equation for the concentration differences:
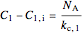 ,
,
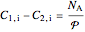 ,
,
 .
.
Adding these equations together and solving for 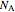 gives the flux in terms of series resistances:
gives the flux in terms of series resistances:
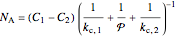 .
.
For more information on how these equations were derived, view the screencast videos [1, 2]. For an example problem, view the screencast video [3].
References
[1] University of Colorado Boulder. Membrane Transport: Series Resistances Part 1 [Video]. (Mar 20, 2017) www.youtube.com/watch?v=hlJA-St-x5w&t=36s.
[2] University of Colorado Boulder. Membrane Transport: Series Resistances Part 2 [Video]. (Mar 20, 2017) www.youtube.com/watch?v=xMl7_tXOSMQ.
[3] University of Colorado Boulder. Membrane Transport: Series Resistances Part 3 [Video]. (Mar 20, 2017) www.youtube.com/watch?v=NEroL-x_g-M.
Permanent Citation