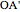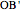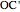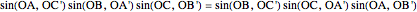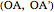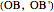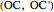Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Menelaus' and Ceva's Theorem for Spherical Triangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

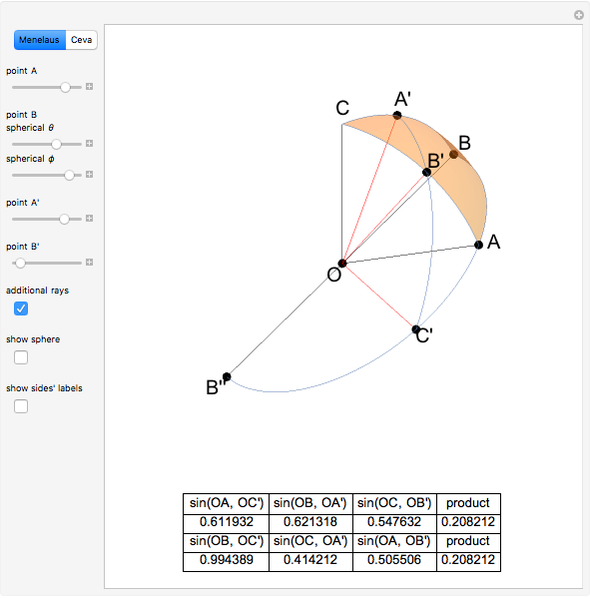
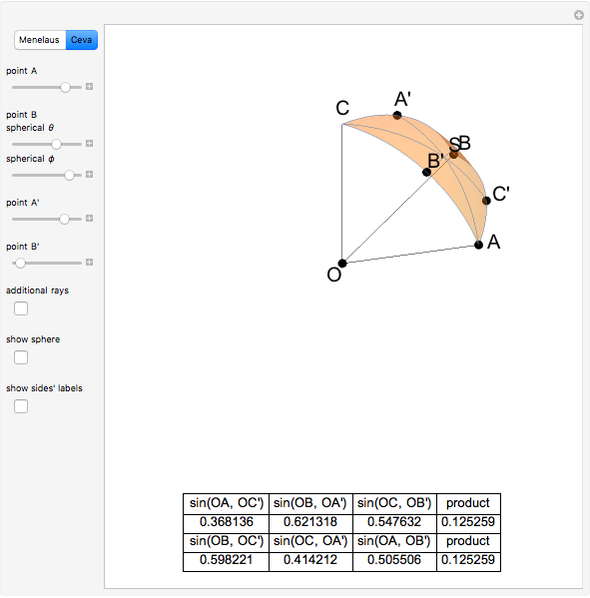
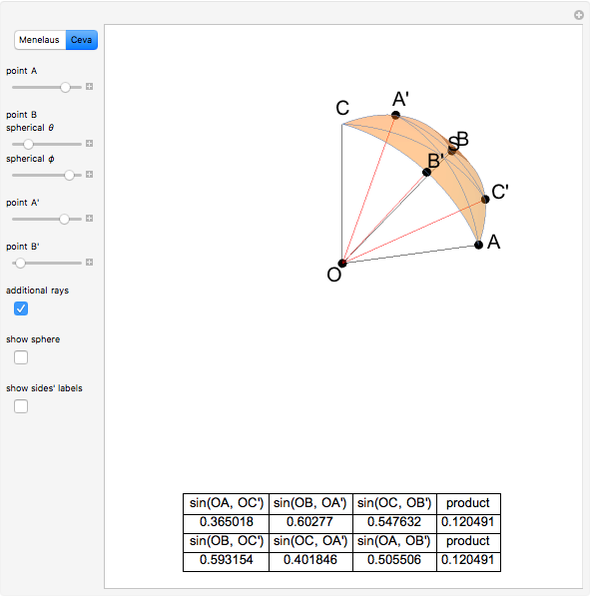
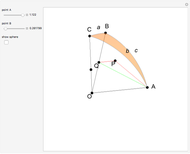
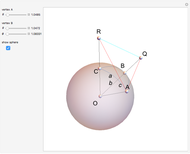
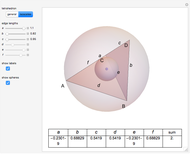
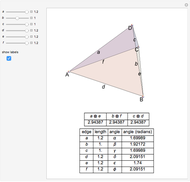
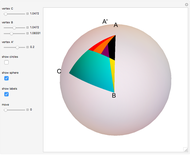
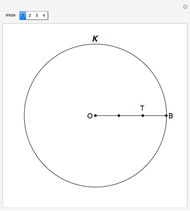
Draw a spherical triangle 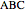on the surface of a unit sphere centered at 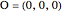. Let the sides opposite the corresponding vertices be the arcs , , and contain the points 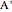, , 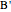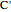. Menelaus's theorem for a spherical triangle states:

[more]

The rays , , are on the same plane if and only if

.

Ceva's theorem for a spherical triangle states:

The planes determined by pairs of rays , and go through the same ray () if and only if

.

[less]

Contributed by: Izidor Hafner (March 2017)
Open content licensed under CC BY-NC-SA

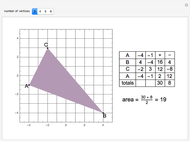
Snapshots

Details

A proof of these theorems can be found in [3, pp. 85–86].

References

[1] Wikipedia. "Spherical Law of Cosines." (Mar 20, 2017) en.wikipedia.org/wiki/Spherical_law_of _cosines.

[2] Wikipedia. "Spherical Trigonometry." (Mar 20, 2017) en.wikipedia.org/wiki/Spherical_trigonometry.

[3] V. V. Prasolov and I. F. Sharygin, Problems in Stereometry (in Russian), Moscow: Nauka, 1989.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send