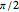Mercator's Instructions: The "Organum Directorium"

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
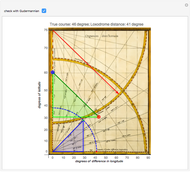
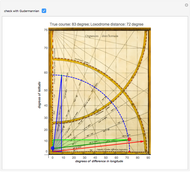
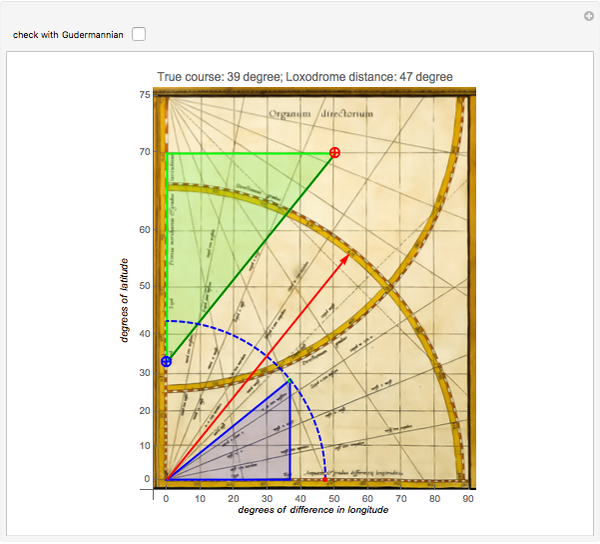
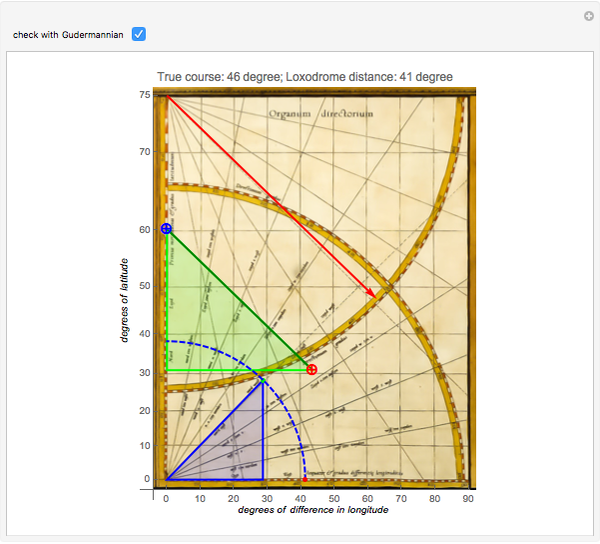
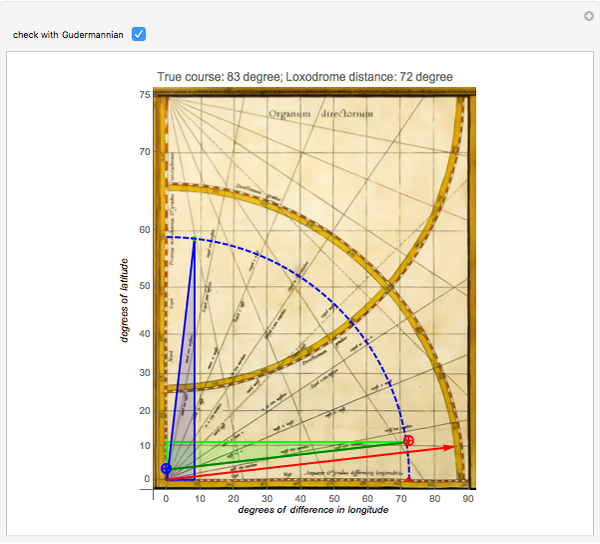
The Flemish cartographer Gerard Mercator was born 500 years ago this year. His revolutionary Mercator projection was first used in his world map of 1569. In this projection, straight loxodromes (lines of constant course) intersect a grid of perpendicular meridians and parallels.
[more]
Contributed by: Erik Mahieu (March 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
One of the three remaining atlases of the world from 1569 is at the Rotterdam Maritiem Museum [2]: maritiemdigitaal.nl.The "Organum Directorium" is on the last page and one can see two strings attached to the upper- and lower-left corners. These strings were an aid to estimate angles and to transfer line lengths.
The entire method is based on the exactness of the "enlarged latitudes" on the 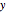 axis. Due to the lack of intellectual property rights in the 16th century, Mercator never published the tables nor the formula by which he calculated these latitudes.
axis. Due to the lack of intellectual property rights in the 16th century, Mercator never published the tables nor the formula by which he calculated these latitudes.
A detailed explanation of the Mercator method can be found in [5].
References
[1] Wikipedia. "Mercator World Map." (Apr 23, 2006) en.wikipedia.org/wiki/File:Mercator_ 1569.png.
[2] G. Mercator, "Nova Et Aucta Orbis Terrae Descriptio Ad Usum Navigantium," Rotterdam Maritiem Museum Atlas, p. 26.
[3] G. Mercator. "Brevis usus Organi Directorii." Ad Maiorem Gerardi Mercatoris Gloriam. (2002) www.wilhelmkruecken.de/ADUSUM/leg10.htm.
[4] B. Kyewski, "Über die Mercatorprojektion: Zum 50jährigen Bestehen des Mercator-Gymnasiums Duisburg," Erdkunde, 5(2), 1951 p. 104.
[5] F. Wilhelm Krücken. "Ad Maiorem Gerardi Mercatoris Gloriam I - V." Ad Maiorem Gerardi Mercatoris Gloriam. (2002) www.wilhelmkruecken.de/b.htm.
Permanent Citation