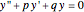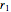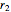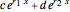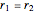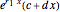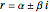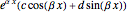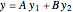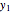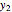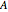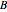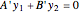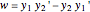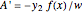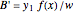Method of Variation of Parameters for Second-Order Linear Differential Equations with Constant Coefficients
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
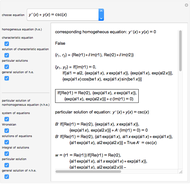
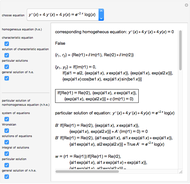
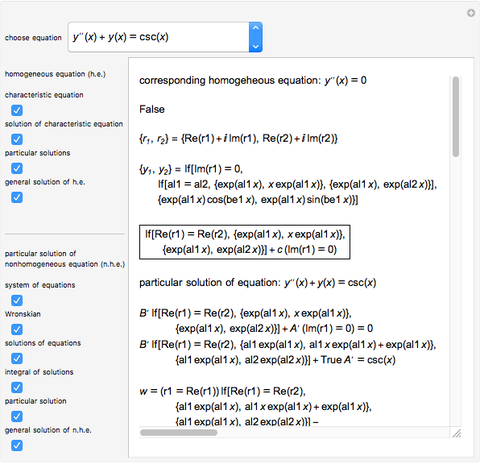
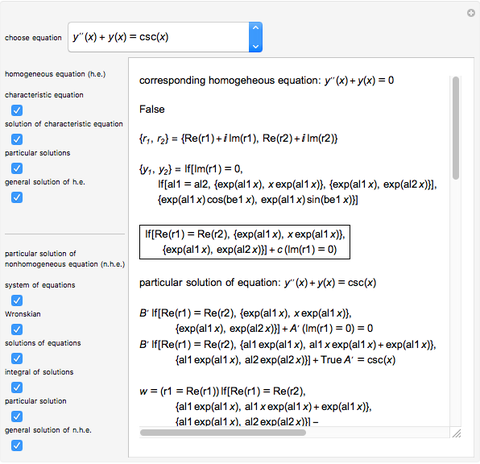
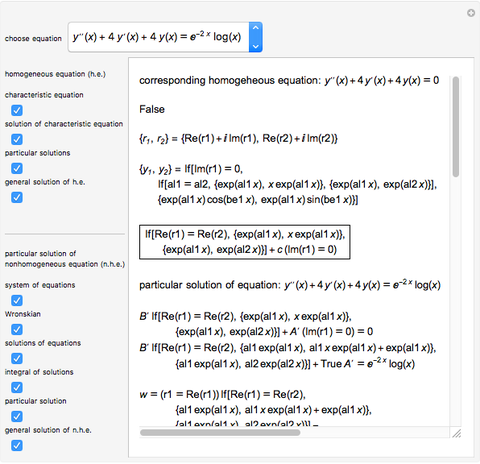
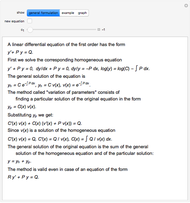
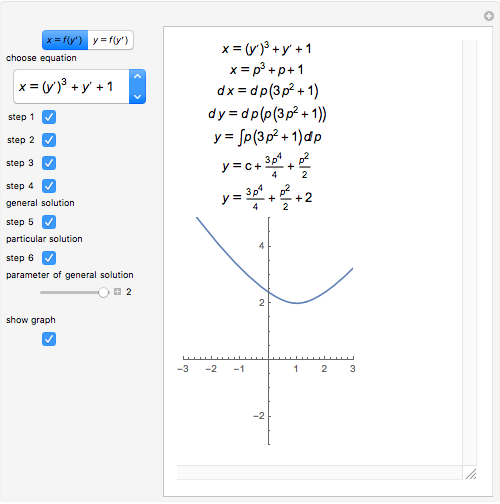
This Demonstration shows how to solve a nonhomogeneous linear second-order differential equation of the form 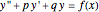 , where
, where 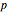 and
and  are constants.
are constants.
Contributed by: Izidor Hafner (April 2014)
Open content licensed under CC BY-NC-SA
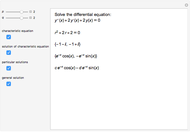
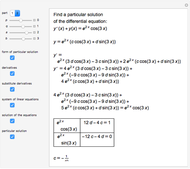
Snapshots
Details
The method of variation of parameters can be used even if 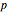 and
and  are not constants.
are not constants.
Reference
[1] V. P. Minorsky, Problems in Higher Mathematics, (Y. Ermolyev, trans.), Moscow: Mir Publishers, 1975 pp. 262–263.
Permanent Citation