Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Michaelis-Menten Enzyme Kinetics of Bi-Bi Reactions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Enzyme kinetics describe the rate of chemical reactions catalyzed by enzymes and the effects of varying the reaction conditions. In an enzymatic reaction, specific molecules bind to an enzyme’s active site and are converted into products. Multiple-substrate reactions are more common than single-substrate reactions, accounting for over 60% of all enzymatic reactions. The following equation represents a bi-bi reaction in which and are substrates, is the enzyme, and and are the products:

[more]

.

Multiple-substrate reactions can be sequential or nonsequential. This Demonstration models the sequential type of reaction. In a sequential reaction, all substrates must bind to the enzyme before the reaction occurs and the products are released. The mechanism of substrate binding in sequential enzymatic reactions can be either random or ordered. This Demonstration explores different reaction conditions that influence enzymatic reactions.

[less]

Contributed by: Bailey Schneider and Matthew Wick (April 2018)
Additional contributions by: Eitan Geva (University of Michigan)
Open content licensed under CC BY-NC-SA

Details

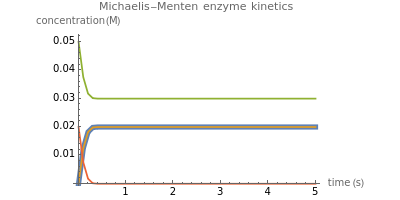
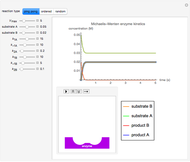
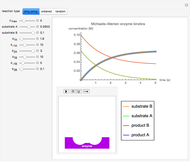
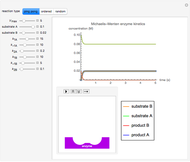
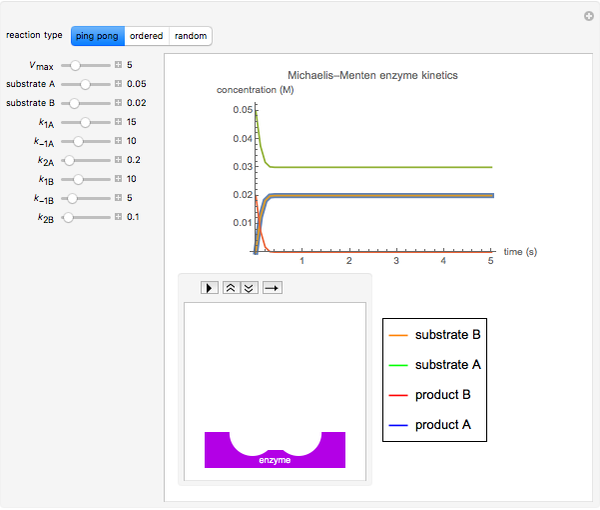
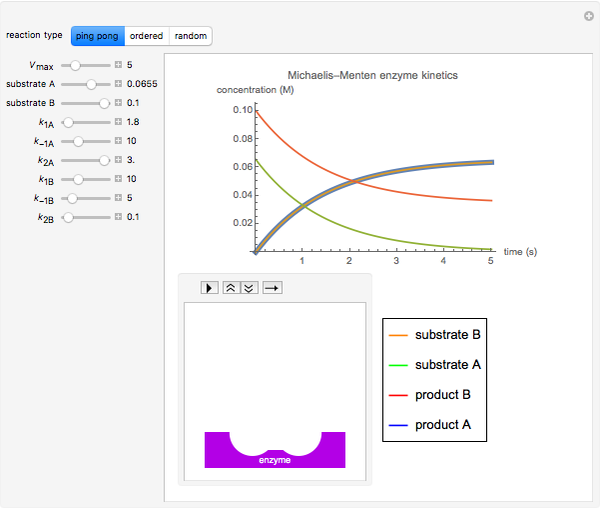
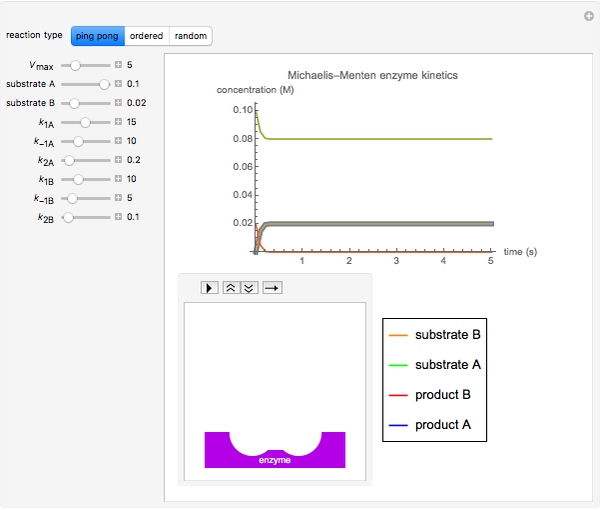
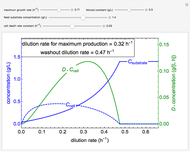
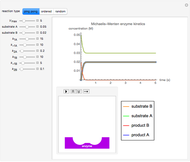
The Demonstration shows the formation of the intermediate complex derived from binding of the free enzyme and two other molecules (substrates and ). This model shows a general sequential reaction involving a single enzyme, two substrates and two products. The Michaelis–Menten enzyme kinetics graph shows a model for rate equations. Use the sliders to explore a variety of reaction conditions, including the initial concentrations of and , various rate constants and . You can choose among three reaction types: ping pong, ordered and random. The lines of the graph represent a Michaelis–Menten steady-state approximation.

References

[1] N. N. Ulusu, "Evolution of Enzyme Kinetic Mechanisms," Journal of Molecular Evolution, 80(5–6), 2015 pp. 251–257. doi:10.1007/s00239-015-9681-0.

[2] S. Tucek, "Choline Acetyltransferase and the Synthesis of Acetylcholine," in The Cholinergic Synapse, Handbook of Experimental Pharmacology, Vol. 86 (V. P. Whittaker, ed.), Berlin, Heidelberg: Springer, 1988 pp. 125–165. doi:10.1007/978-3-642-73220-1_ 7.

Submission from the Compute-to-Learn course at the University of Michigan.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send