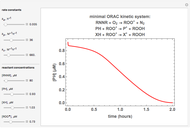
Minimal ORAC Kinetic System: Mathematical Analysis

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Contributed by: Juan B. Arellano, Elena Mellado-Ortega and K. Razi Naqvi (April 2017)
Open content licensed under CC BY-NC-SA
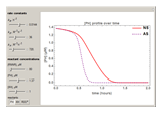
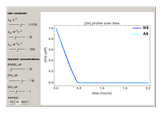
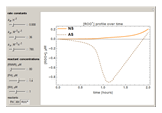
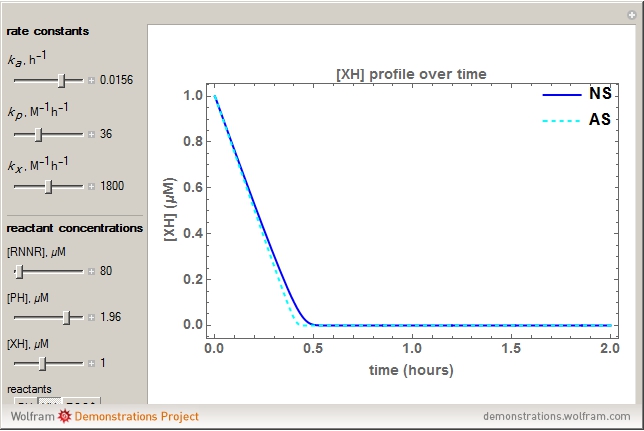
Snapshots
Details
The first-order ODEs that define the minimal ORAC kinetic system can be written [1]:
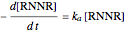 ,
,
 ,
,
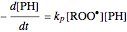 ,
,
 .
.
At  , the concentrations of the starting and intermediate reactants are:
, the concentrations of the starting and intermediate reactants are:
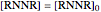 ,
,
 ,
,
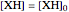 ,
,
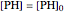 .
.
Following this notation, the concentrations of the azo compound, 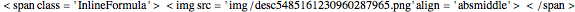 ,
,  and
and  at time
at time  can be represented as:
can be represented as:
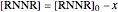 ,
,
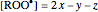 ,
,
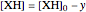 ,
,
 ,
,
where  ,
, 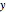 and
and  stand for the reacted concentrations of
stand for the reacted concentrations of 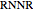 ,
, 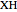 and
and 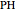 at time
at time  , respectively.
, respectively.
The built-in function ParametricNDSolve was used to find numerical solutions to the given differential equations applying the Runge–Kutta method. However, an exact analytical solution of the ODEs of the minimal ORAC kinetic system was not possible applying Lie symmetry theory. The mathematical form of the coefficients of the nonautonomous Chini equation, an ODE that appears after some mathematical transformations and is polynomial in the dependent variable, precluded the reduction of this equation to the autonomous Chini equation. However, an approximate analytical solution was found when 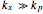 . In this former case, the nonautonomous Chini equation was transformed into a nonhomogenous ODE that was linear in the dependent variable. The dependence of the concentration profile of
. In this former case, the nonautonomous Chini equation was transformed into a nonhomogenous ODE that was linear in the dependent variable. The dependence of the concentration profile of 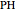 and
and 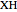 on time and initial conditions was found to be:
on time and initial conditions was found to be:
 ,
,
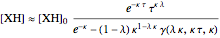 ,
,
where  ,
, 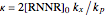 ,
, 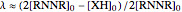 and
and  stands for the lower incomplete gamma function.
stands for the lower incomplete gamma function.
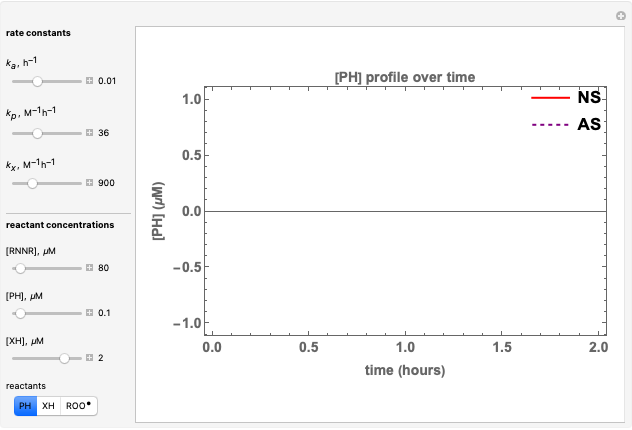
The concentration profile over time of the peroxyl radical was a sum of terms:
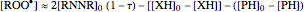 .
.
Reference
[1] J. B. Arellano, E. Mellado-Ortega and K. R. Naqvi, "The ORAC Assay: Mathematical Analysis of the Rate Equations and Some Practical Considerations," International Journal of Chemical Kinetics, forthcoming.
Permanent Citation