Miter Joint and Fold Joint

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
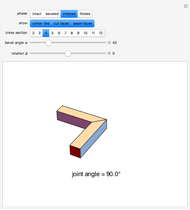
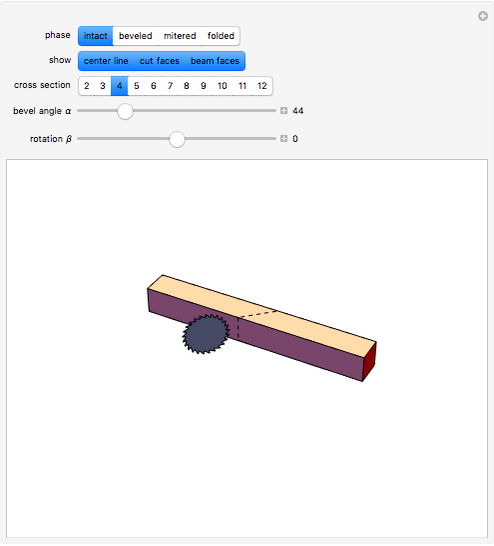
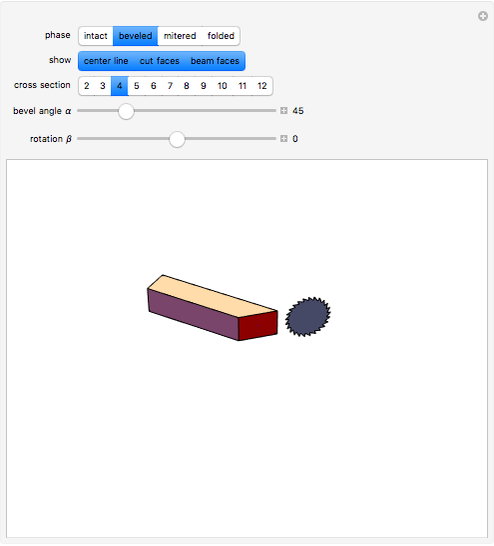
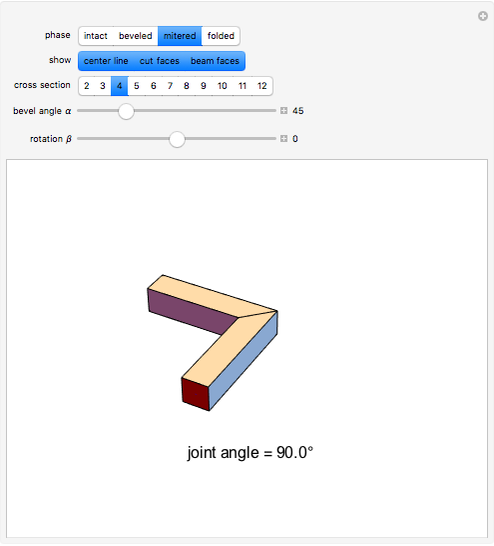
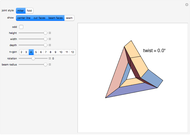
This Demonstration shows the process of forming a miter joint or fold joint by beveling a beam at an angle and connecting it to another similarly beveled beam. The cross section of the beam can be varied, as can the bevel angle and the longitudinal rotation of the beam. A fold joint in a solid beam (i.e., not a strip with 2-gon as cross section) involves self-intersection.
Contributed by: Tom Verhoeff (Eindhoven University of Technology) (March 2011)
Inspired by the artwork of: Koos Verhoeff
Open content licensed under CC BY-NC-SA
Snapshots
Details
These miter and fold joints connect two beams with the same cross section. In this Demonstration, the cross section is a regular polygon, but this joint applies to any polygon. In the case of the miter joint, the cut face lies in the interior bisector plane of the angle spanned by the two beams. For the fold joint, it lies in the exterior bisector plane, where the cut face can be viewed as a mirror that reflects a light ray along the center line of the beam.
For a fold joint in a beam with a 2-gon as cross section (i.e., a strip) it is not necessary to cut the beam. It suffices to score the strip at the bevel angle and fold it over appropriately. Folding a beam whose cross section has a nonzero area involves self-intersection: each of the beam's faces is folded separately.
Permanent Citation
"Miter Joint and Fold Joint"
http://demonstrations.wolfram.com/MiterJointAndFoldJoint/
Wolfram Demonstrations Project
Published: March 7 2011