Miura Map Folding and Unfolding

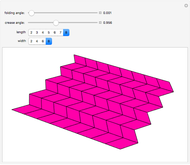
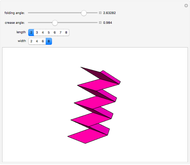
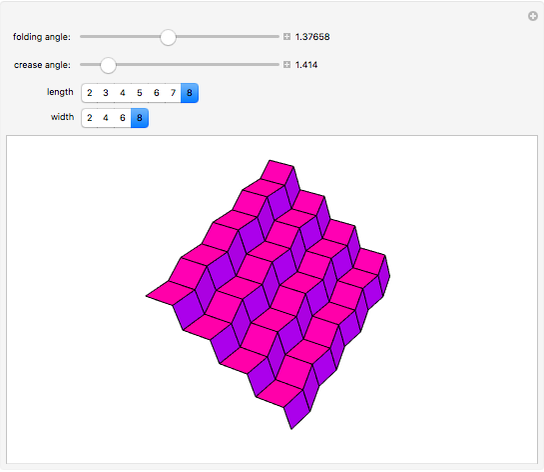
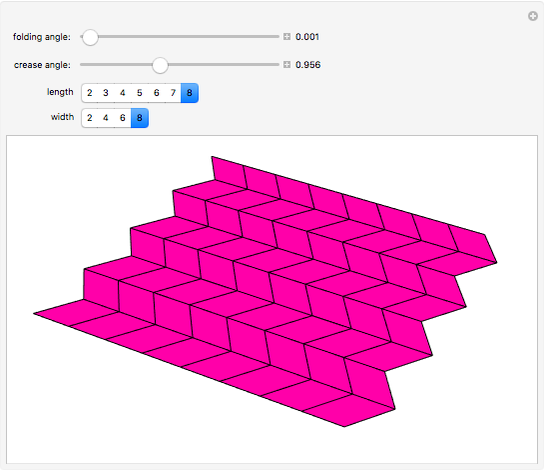
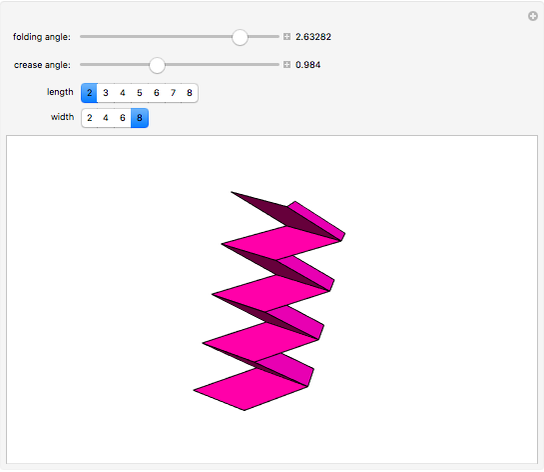
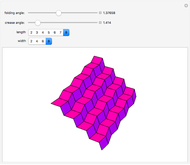
The Miura map fold (aka Miura-ori) is an example of a rigid origami model (can be folded from sheet metal with hinges instead of crease lines) which has applications in solar panel design for space satellites. This Demonstration offers a proof, of sorts, that the Miura map fold is rigid when made from a tiling of any nonsquare parallelogram.

Contributed by: Thomas C. Hull

Show Initialization Code

(24 lines omitted)

The folding angle represents the angle by which one specific crease is folded, which then determines the folding angles of all the other creases (folding angle =

- the dihedral angle of the crease). The crease angle is the acute angle of the parallelogram which is tiled to make the crease pattern. The value crease angle =

is a singularity of the folding equations; the creases cannot all collapse simultaneously when the parallelograms are perfect squares (they would have to be folded sequentially, like a regular road map). For some history of the Miura map fold, more information is online.