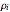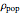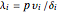Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Mixing and Infection in a Two-Group SIS Model

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Consider a population composed of two groups of equal size (designated 1 and 2), in which individuals can be either "infected" or "susceptible." In each time period, each individual has a probability of interacting with another individual. With probability 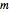, this interaction is with an individual of the other group. Susceptible individuals become infected only if they interact with an infected individual, and in that case they do so with probability , where denotes the individual's group. Infected individuals become susceptible with probability .

[more]

This Demonstration shows the proportion of infected individuals in each group (and in the total population ) at the nearly globally asymptotically stable state of the mean dynamics, as a function of the level of mixing between the two groups (i.e. the percentage of interactions that occur between individuals of different groups). The two relevant parameters are the effective infection rates of each group: .

[less]

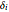Contributed by: Segismundo S. Izquierdo, Luis R. Izquierdo and Dunia López-Pintado  (January 2018)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The evolution of the fraction of infected individuals in group 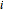over time is described by the following system of nonlinear differential equations:

,

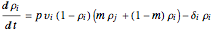where and 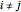. These equations can be rewritten as:

.

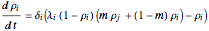This model is analyzed in detail in [1].

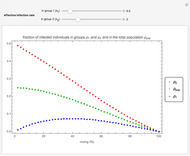
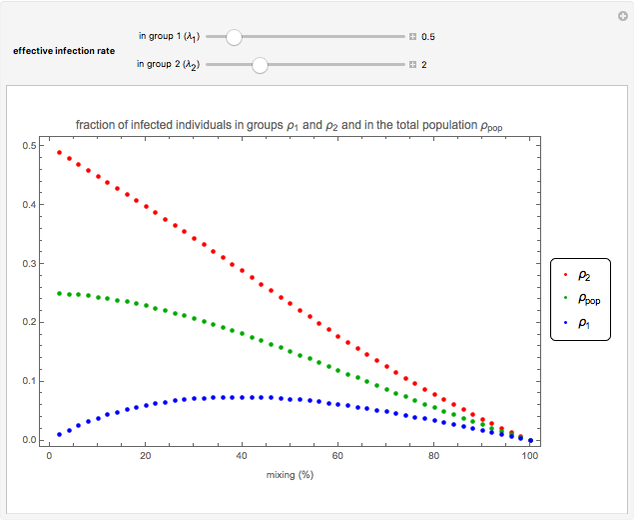
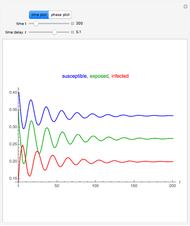
Snapshot 1: by increasing the population mixing beyond 40%, the infection level decreases in both groups

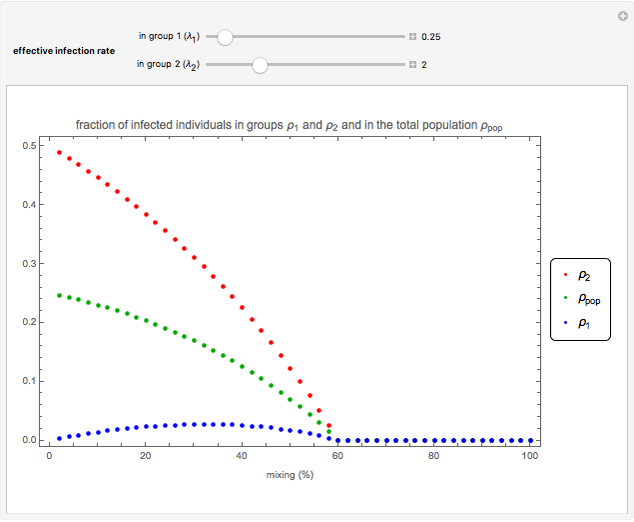
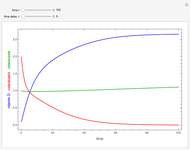
Snapshot 2: by increasing the population mixing beyond 33%, the infection level decreases in both groups, until the mixing level is greater than 60%, in which case the infection dies out in the whole population

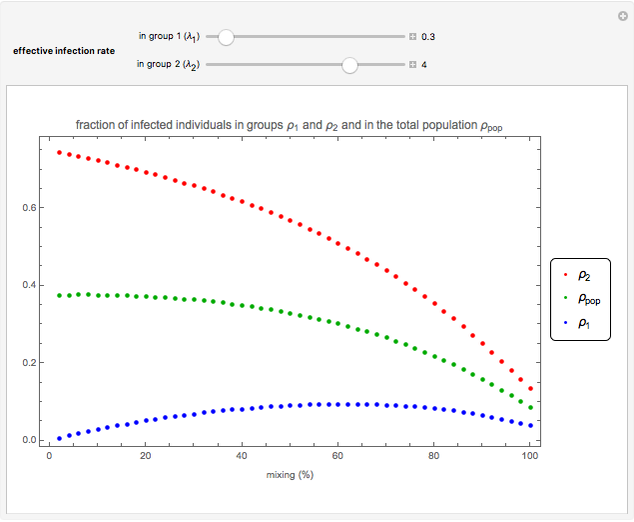
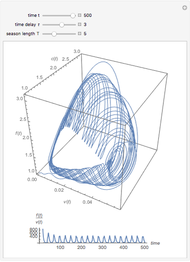
Snapshot 3: by increasing the population mixing beyond 62%, the infection level decreases in both groups, but the infection never dies out completely

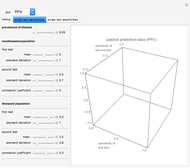
Snapshot 4: An increase in mixing always benefits the sensitive group (i.e. group 2, since ) at the expense of the resistant group. The total population infection level is maximal at an intermediate level of mixing.

Snapshot 5: An increase in mixing always benefits the sensitive group (i.e. group 2, since ) at the expense of the resistant group. The total population infection level increases with mixing.

Reference

[1] S. S. Izquierdo, L. R. Izquierdo and D. López-Pintado, "Mixing and Diffusion in a Two-Type Population." Royal Society Open Science 5(2) 172102. (2018) dx.doi.org/10.1098/rsos.172102.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send