Details

An alphabet in an information system contains 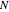letters (or possible outcomes). Let 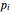(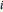=1 to 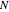) denote the probabilities for each of these letters to occur in an information-containing register. Here, 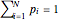, and we can detect a letter by measuring the information-containing register (or cell).

In an ideal system, the register can accommodate exactly one letter of an alphabet. Each measurement thus yields a value and possible outcomes are defined by the letters known from previous observation. These letters may succinctly express complex states containing a string of correlated information.

Now, a new type of disorder is introduced into this system if a register is allowed to deform, and as a result, contain more than one letter (or perhaps fractional letters).

If the deformation is measured by , then the probability that a cell still contains a pure predefined letter is given by 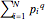, which is less than the previous sum and less than unity.

The new degree of freedom, and thus disorder, in the information measurement system is introduced by the existence of "mixed letters" in the cell.

The Shafee Mixing Entropy, defined by the author, measures the degree of uncertainty introduced in information measurement as a consequence of such deformations of information containing cells or because of deformation at the information/measurment interface.

The entropy is given by 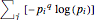, where 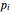is the original probability of the letter to occupy an undeformed cell.

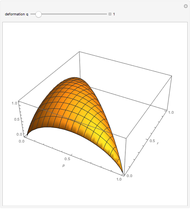
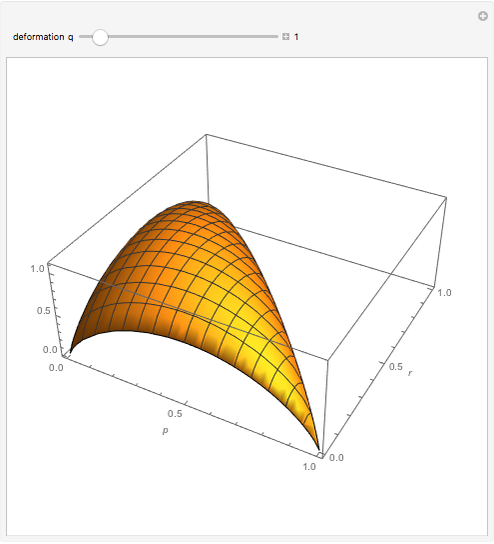
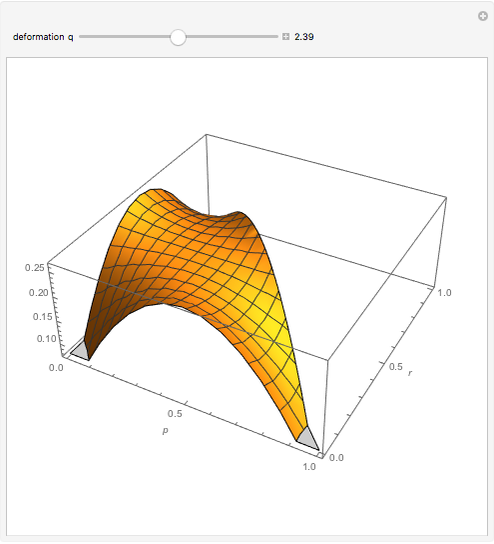
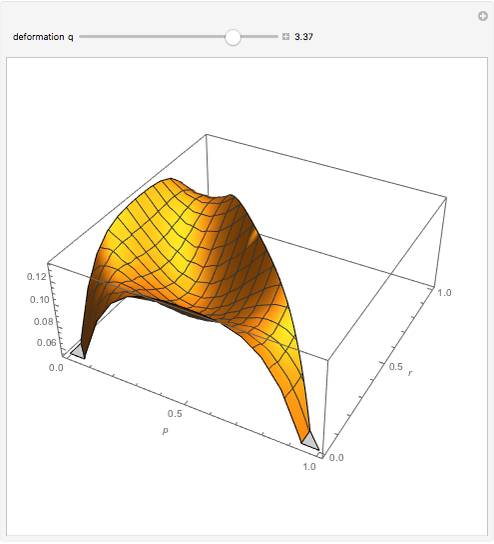
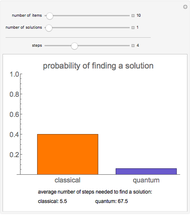
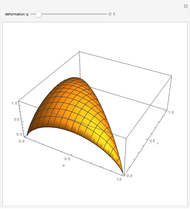
In this Demonstration, the mixing entropy is plotted for the case of a three-letter alphabet. The degree of deformation of a cell, , is allowed to vary between .8 and 4. It is interesting to note that near = 2.5, the symmetric case (where all the letters have the same probability of occurring in the cell) ceases to give the highest entropy. Rather, a pattern emerges where the symmetric case gives a local maximum and global maxima occur near the endpoints (where one of the letters has a very low probability of occurring in the cell).

Such mixing of states and disorder may have applications in studies of complexity and emergent phenomena.

References:

F. Shafee, "Lambert Function and a New Nonextensive Form of Entropy," IMA Journal of Applied Mathematics, 72(6), 2007 pp. 785–800.

F. Shafee, "Generalized Entropy from Mixing: Thermodynamics, Mutual Information and Symmetry Breaking," arXiv.org.