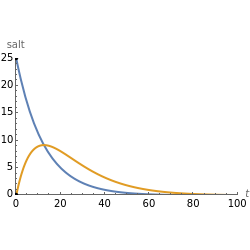
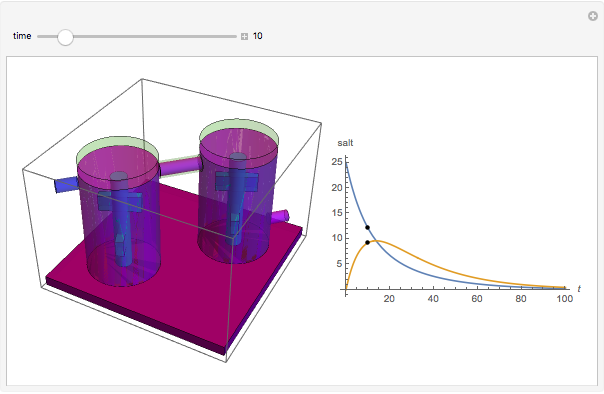
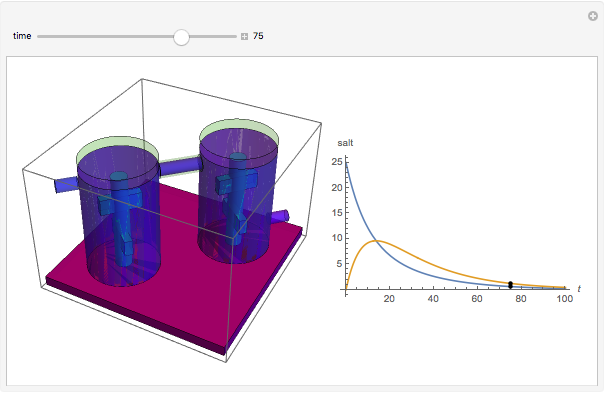
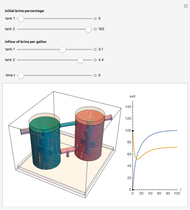
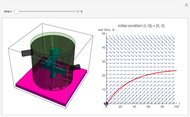
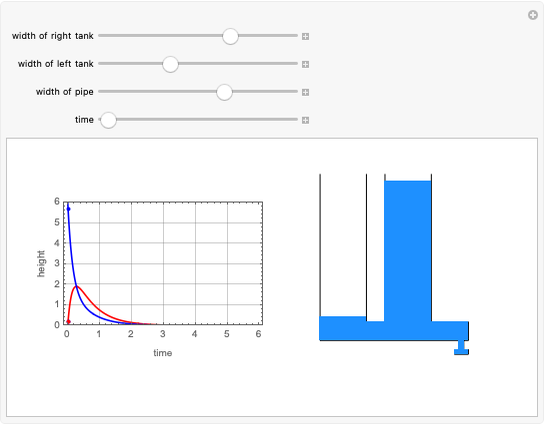
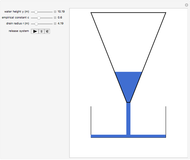
Tank A contains 50 liters of brine in which 25 grams of salt are dissolved. Tank B contains 50 liters of brine in which 0 grams of salt are dissolved. Fresh water is pumped into tank A at a rate of 4 liters/minute; the well-mixed solution is pumped from tank A into tank B at 4 liters/minute. The well-mixed solution from tank B is pumped out at 4 liters/minute. This Demonstration uses colors and animation to visualize the solution to this problem.
This problem was taken from the MA205 course examples at the United States Military Academy, West Point. It involves a model of a multi-tank mixing problem using a system of first-order differential equations. Students are asked to solve the equations using a variety of methods. This Demonstration provides a visualization of the mixing example given as a reading assignment to help prepare the students. This problem would be a good example for any course that includes coupled first-order differential equations. It lets an instructor simulate a visual experiment without the mess of setting up a lab in the classroom. Students can solve these equations using a variety of methods including numerical, Laplace transforms, eigenvalues and eigenvectors, and elimination.
Reference
D. Zill, A First Course in Differential Equations with Modeling Applications, 9th ed., Pacific Grove, CA: Thomson Brooks/Cole, 2008.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
