Modeling Parasitoid-Host Dynamics with Delay Differential Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
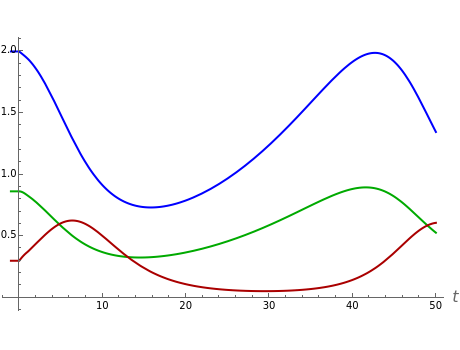
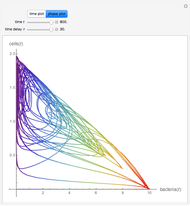
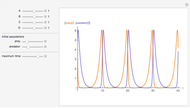
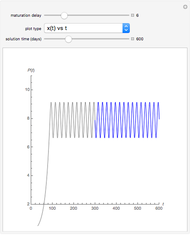
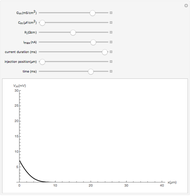
A parasitoid is an organism that inhabits a host organism. Unlike a true parasite, however, it ultimately sterilizes or consumes the host, a more dire prognosis for the host.
[more]
Contributed by: Ferdinand Pfab (December 2015)
Open content licensed under CC BY-NC-SA
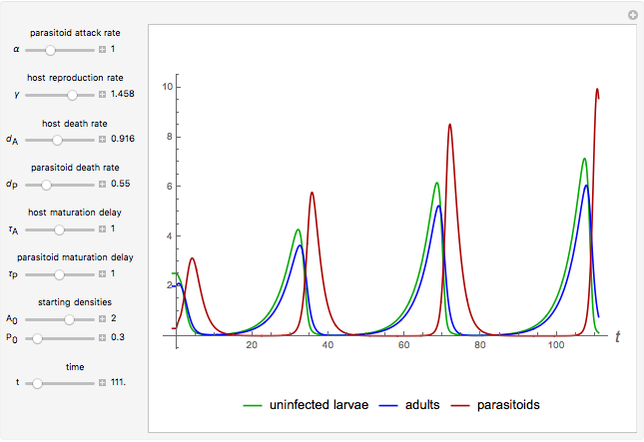
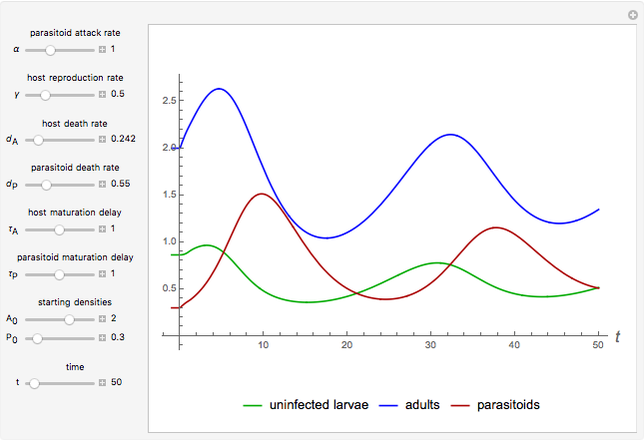
Snapshots
Details
For 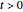 , the system of equations is
, the system of equations is
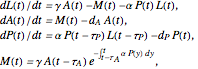
where
 : time
: time
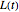 : uninfected host larva density
: uninfected host larva density
 : host adult density
: host adult density
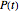 : parasitoid adult density
: parasitoid adult density
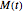 : rate of host larvae maturating to host adults
: rate of host larvae maturating to host adults
 : attack rate of parasitoids
: attack rate of parasitoids
 : rate of larva production for host adults
: rate of larva production for host adults
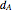 : death rate of host adults
: death rate of host adults
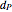 : death rate of parasitoids
: death rate of parasitoids
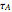 : maturation delay for noninfected larvae
: maturation delay for noninfected larvae
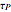 : maturation delay for infected larvae
: maturation delay for infected larvae
To start the system, we set constant adult host and parasitoid densities (for 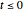 )
)
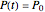 ,
,
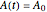 ,
,
and calculate the beginning larva density consistently (for 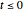 )
)
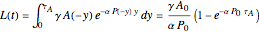 .
.
A note on the implementation: in order to numerically solve the system of delay differential equations with the Mathematica built-in function NDSolve, we calculate the integral in the formula for 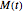 by introducing another state variable
by introducing another state variable
 ,
,
which we define for 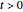 by
by
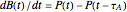
and for 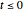 by
by
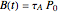 .
.
Reference
[1] W. W. Murdoch, R. M. Nisbet, S. P. Blythe, W. S. C. Gurney, and J. D. Reeve, "An Invulnerable Age Class and Stability in Delay-Differential Parasitoid-Host Models," The American Naturalist, 129(2), 1987 pp. 263–282. www.jstor.org/stable/2462003.
Permanent Citation