Moduli Space of Shapes of a Tetrahedron with Faces of Equal Area

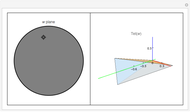
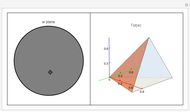
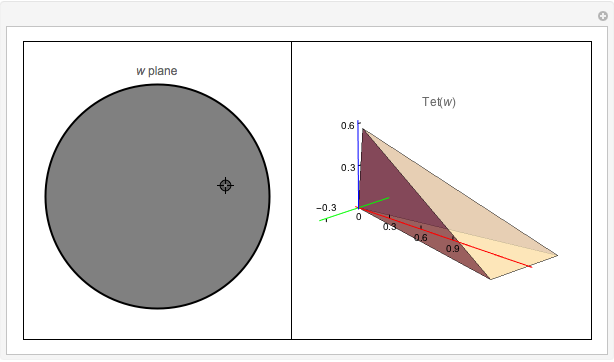
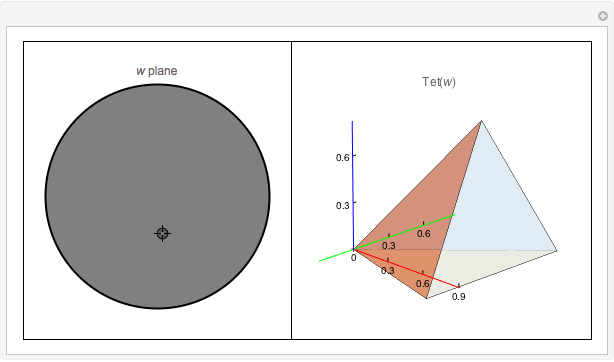
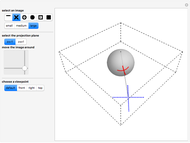
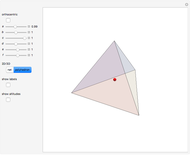
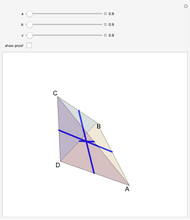
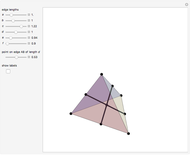
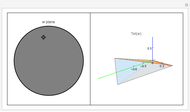
The space of shapes of a tetrahedron with fixed face areas is naturally a symplectic manifold of real dimension two. This symplectic manifold turns out to be a Kahler manifold and can be parametrized by a single complex coordinate given by the cross ratio of four complex numbers obtained by stereographically projecting the unit face normals onto the complex plane. This Demonstration illustrates how this works in the simplest case of a tetrahedron whose four face areas are equal. 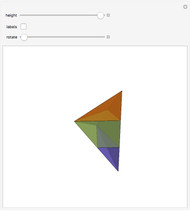For convenience, the cross-ratio coordinate is shifted and rescaled to so that the regular tetrahedron corresponds to , in which case the upper half-plane is mapped conformally into the unit disc . The equi-area tetrahedron is then drawn as a function of the unit disc coordinate .