Molecular Point Groups

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
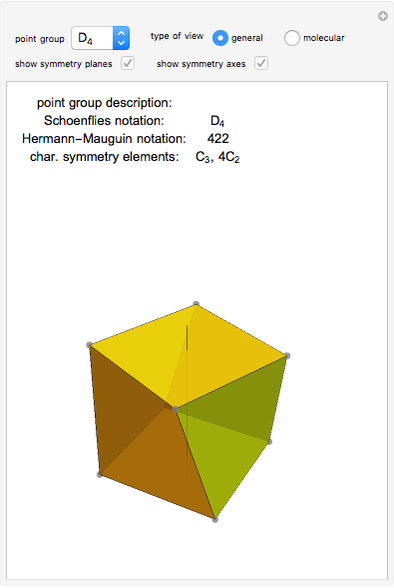
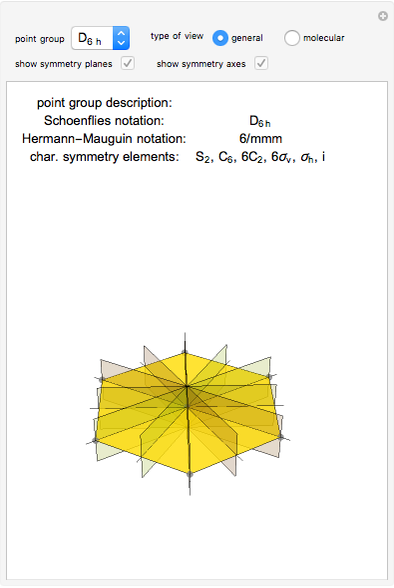
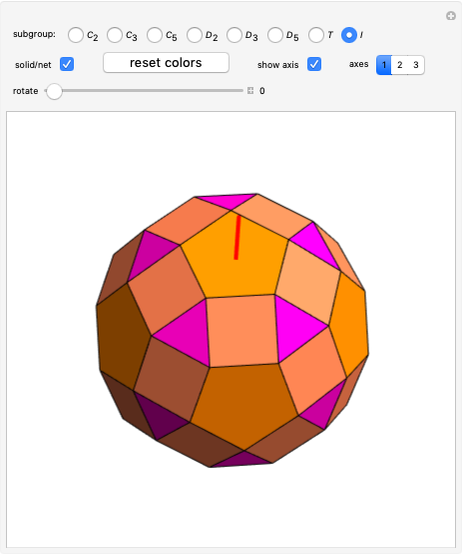
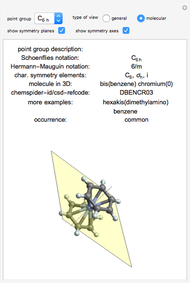
The symmetry elements and operations characterizing the geometry of a molecule form a point group. The possible symmetry elements are: the identity element,  -fold axis of symmetry, plane of symmetry, center of inversion, and
-fold axis of symmetry, plane of symmetry, center of inversion, and  -fold rotation-reflection axis.
-fold rotation-reflection axis.
Contributed by: Guenther Gsaller (May 2012)
(Institute of Organic Chemistry, Johannes Kepler University, Linz, Austria, http://www.jku.at/orc/)
After work by: Magdolna Hargittai, István Hargittai, Ulrich Müller, Gary L. Miessler
Open content licensed under CC BY-NC-SA
Snapshots
Details
Mathematicians developed abstract group theory in the early 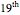 century. In the 1920s and 1930s the theory of molecular symmetry was applied to atoms, molecules, and crystals. The Hermann–Mauguin notation is most often used to describe the symmetries in crystals, while for molecules and their spectroscopic properties the Schönflies notation is preferred.
century. In the 1920s and 1930s the theory of molecular symmetry was applied to atoms, molecules, and crystals. The Hermann–Mauguin notation is most often used to describe the symmetries in crystals, while for molecules and their spectroscopic properties the Schönflies notation is preferred.


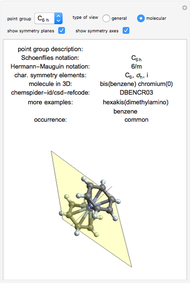
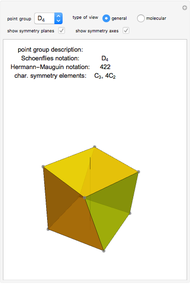
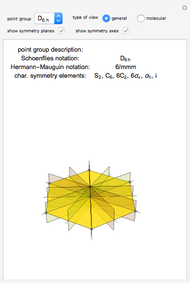
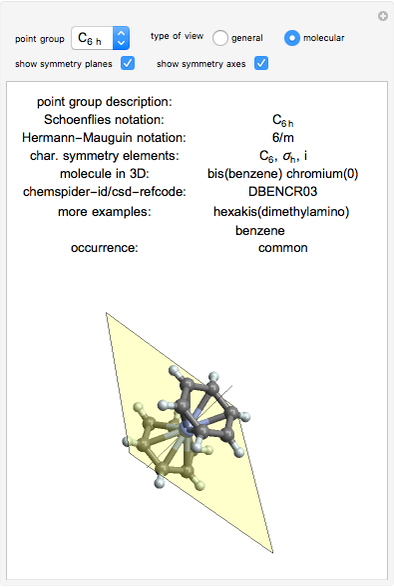
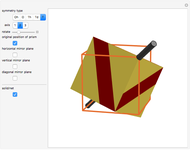
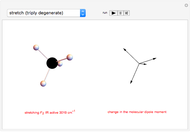
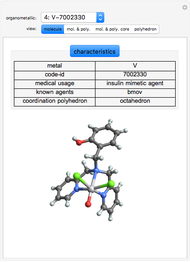
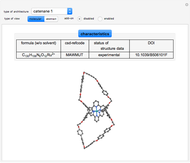
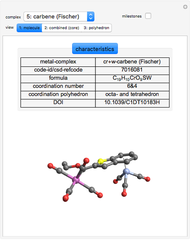
Use the "type of view" radio button to show a ball-and-stick figure of a molecule with the same molecular point group. In molecular view, the checkboxes "show symmetry planes" and "show symmentry axes" are enabled. Chemical names for further examples are listed, if available.
ChemSpider and CSD are the sources for the ball and stick figures. The ChemSpider IDs and CCDC refcodes for each used structure are listed in the Demonstration.
References
[1] M. Hargittai and I. Hargittai, Symmetry through the Eyes of a Chemist, New York: Springer, 2009.
[2] U. Müller, Inorganic Structural Chemistry, New York: J. Wiley & Sons, 2006.
[3] G. Miessler and D. Tarr, Inorganic Chemistry, NJ: Prentice-Hall, 2004.
[4] G. Lawrance, Introduction To Coordination Chemistry, New York: J. Wiley & Sons, 2010.
[5] M. Hollas, Modern Spectroscopy, New York: J. Wiley & Sons, 2004.
[6] D. Johnston. "Gallery." Symmetry @ Otterbein. (May 2012) symmetry.otterbein.edu/gallery/index.html.
[7] S. Immel. "Molecular Structures of Organic Compounds - Symmetry and Point Groups." Technische Universitat Darmstadt. (May 2012) csi.chemie.tu-darmstadt.de/ak/immel/tutorials/symmetry/index.html.
[8] Wikipedia. "Punktgruppen in der Molekülphysik." (May 2012) de.wikipedia.org/wiki/Punktgruppe# Punktgruppen_in _der _Molek.C3.BClphysik.
Permanent Citation