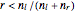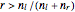Molecules Distributed between Two Compartments

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
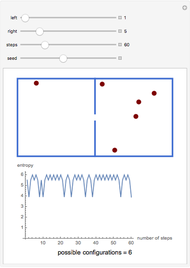
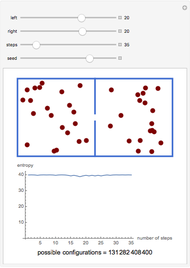
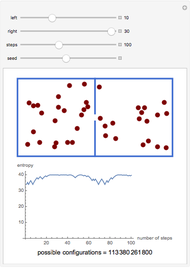
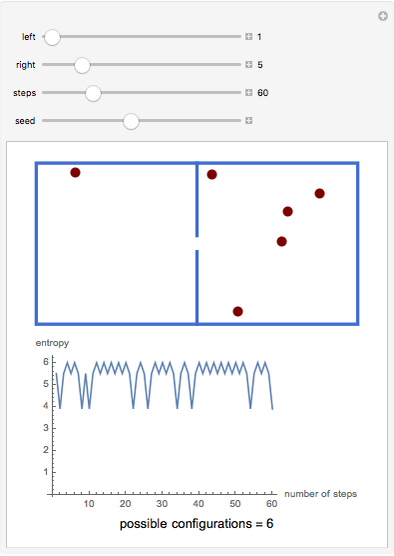
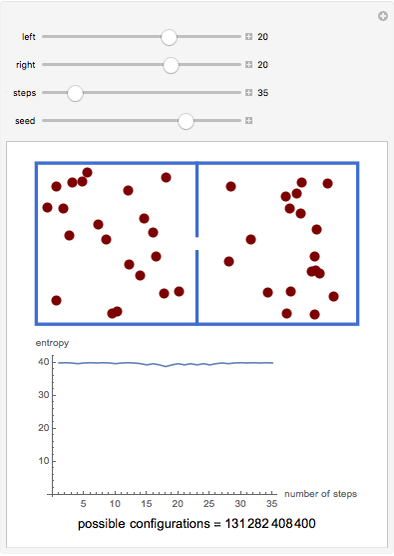
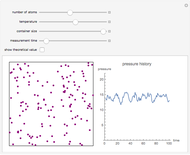
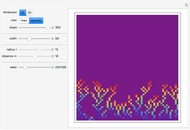
A box has two compartments connected by a hole. There are 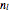 molecules in the left compartment and
molecules in the left compartment and 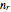 in the right.
in the right.
Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
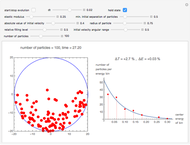
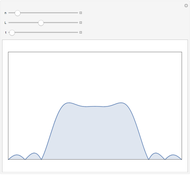
The entropy is 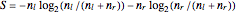 .
.
The number of possible configurations for a particular number of particles in the left compartment is equal to the binomial coefficient 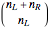 .
.
This experiment is quoted by Stephen Wolfram as an early inspiration that led him to write A New Kind of Science.
References:
F. Reif, Statistical Physics, Berkeley Physics Course, Vol. 5, New York: McGraw-Hill, 1967.
R. M. Eisberg and L. S. Lerner, Physics: Foundations and Applications, Vol. 2, New York: McGraw-Hill, 1981.
See Statistical Mechanics and Microstate on Wikipedia for more information.
Permanent Citation