Moral Hazard and Least-Cost Contracts: Impact of Changes in Conditional Probabilities

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Moral hazard (often called hidden action) arises when one party (a principal) hires another party (an agent) who undertakes unobservable effort. The agent's effort is stochastically related to the outcomes or profits of the principal. Because the effort is not observable or verifiable, the agent can only be paid a wage contingent upon the observable variable, such as whether a sale occurred or not. If a profit-maximizing principal wants the agent to work hard, she must provide a contract that (i) induces the agent to accept it, and (ii) induces the agent to work hard rather than shirk. The former is often called "individual rationality" or "participation constraint" and is satisfied if the agent's expected utility is at least equal to his reservation utility. The latter is called "incentive compatibility" and is satisfied if the agent's expected utility from working hard is at least equal to his expected utility from shirking.
Contributed by: Randy Silvers (Deakin University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
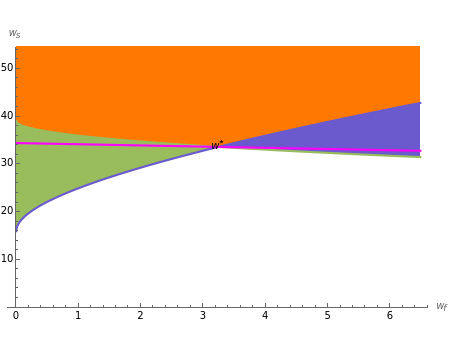
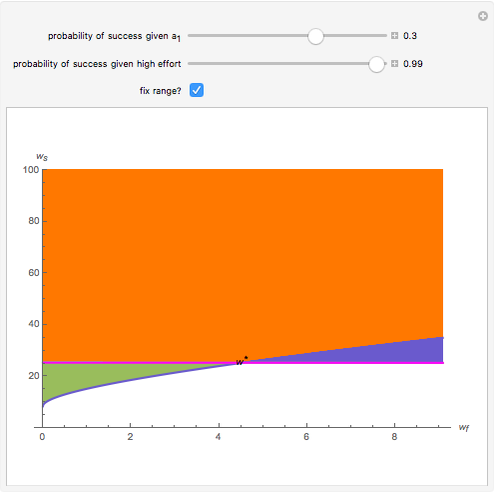
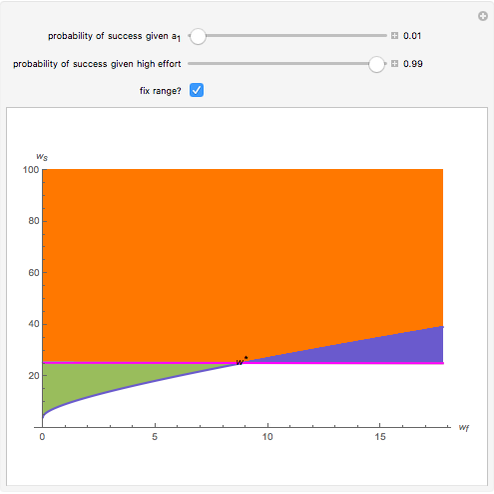
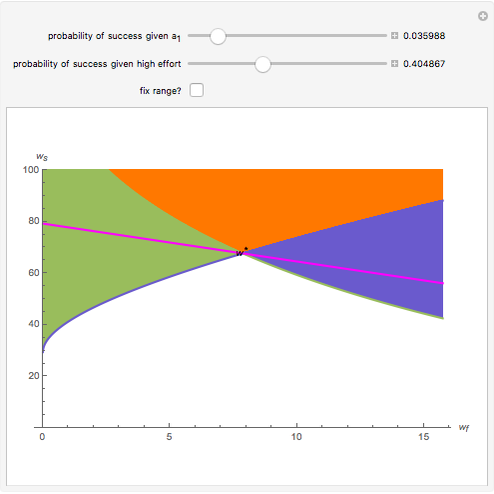
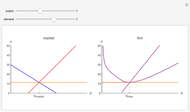
A contract pays 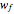 if the outcome is a "failure" and
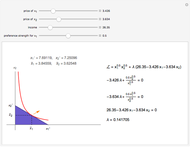
if the outcome is a "failure" and 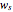 if the outcome is a "success", so that each point in the quadrant is a possible contract. The Demonstration shows the regions of contracts that are:
if the outcome is a "success", so that each point in the quadrant is a possible contract. The Demonstration shows the regions of contracts that are:
(i) incentive compatible but not individually rational (green);
(ii) individually rational but not incentive compatible (blue); and
(iii) both (orange).
It also shows the optimal least-cost contract and, implicitly, the expected cost.
The green negatively sloped line represents the locus of contracts that just satisfy individual rationality; that is, the agent receives exactly his reservation utility. The blue positively sloped line represents the locus of contracts that just satisfy incentive compatibility; that is, the agent is indifferent between choosing 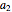 and choosing the minimum effort,
and choosing the minimum effort, 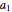 . The purple line represents a locus of contracts that cost the principal the same amount.
. The purple line represents a locus of contracts that cost the principal the same amount.
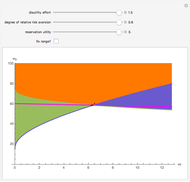
These change as the disutility of effort 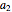 , reservation utility
, reservation utility 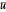 , and degree of relative risk aversion
, and degree of relative risk aversion  , change. Where
, change. Where 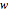 is the agent's wage and
is the agent's wage and  is the disutility of his effort, the agent's utility is given by
is the disutility of his effort, the agent's utility is given by  .
.
The expected cost of the contract is directly proportional to the intercept of the purple line. Pay attention to the values on both axes and the size of the region. Notice what happens to the purple and green lines as the degree of relative risk aversion approaches 0; also notice that everywhere, 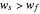 .
.
The model assumes that 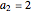 and
and  . The agent's utility is square-root utility (his utility equals the square root of his wage) so that
. The agent's utility is square-root utility (his utility equals the square root of his wage) so that  ; the degree of relative risk aversion is
; the degree of relative risk aversion is 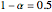 .
.
Permanent Citation