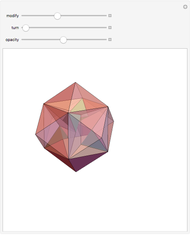
Morphing the Császár Polyhedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
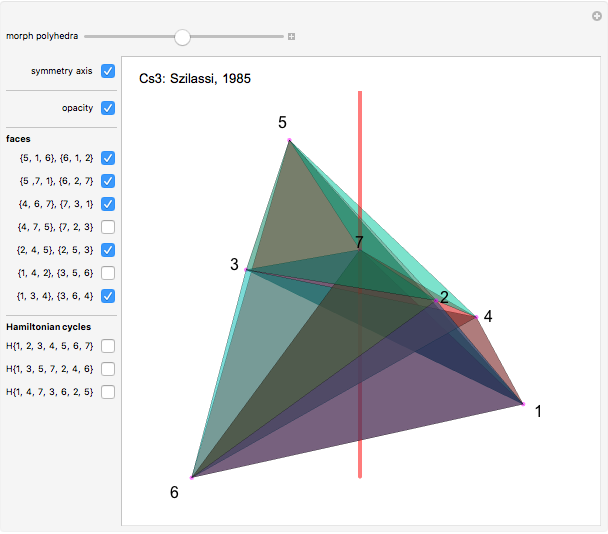
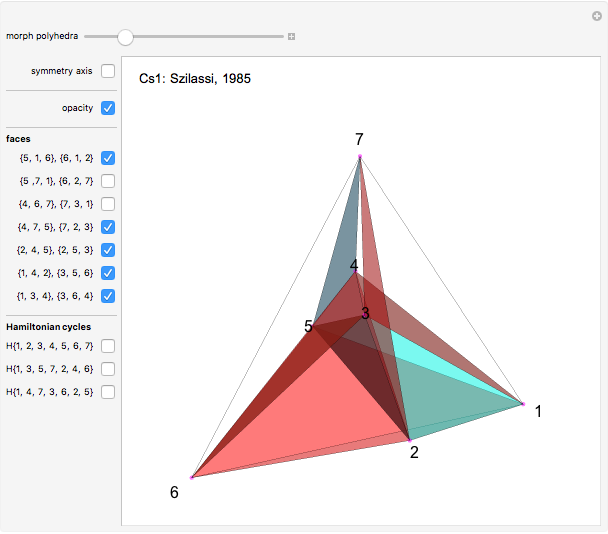
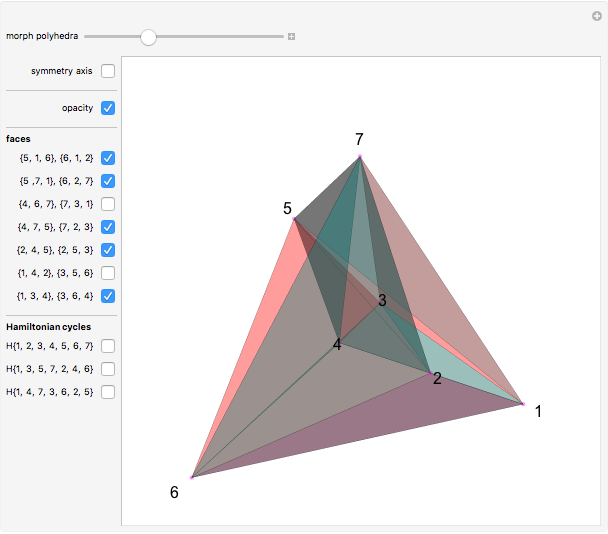
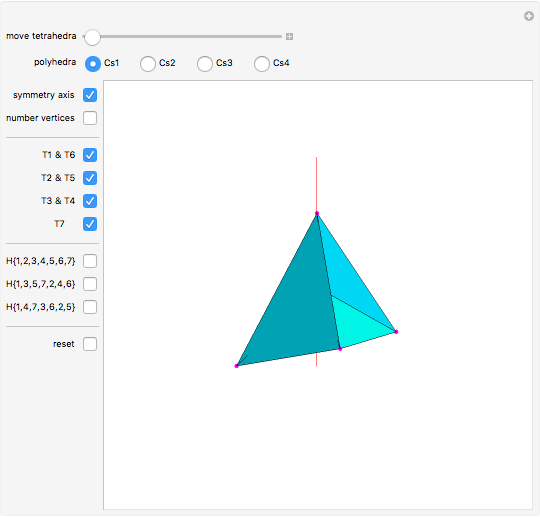
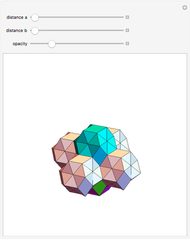
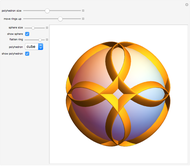
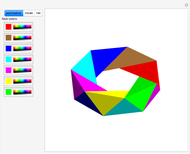
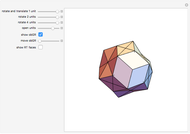
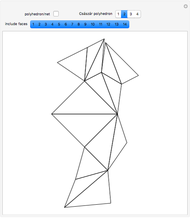
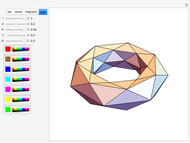
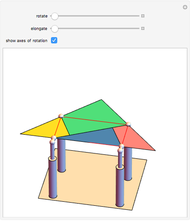
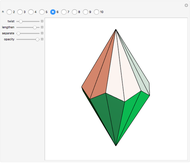
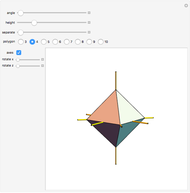
Four versions of the Császár polyhedron are shown. You can study the transition between these versions. In each of the four, the triangles shared by adjacent tetrahedra form a Möbius band. Each Möbius band contains all seven vertices of the Császár polyhedron, but only 14 of its edges. The edges of the Möbius graph form three Hamiltonian cycles, which are exactly loops, if the faces of the polyhedron do not intersect one another. If the faces intersect one another and the edges do not intersect one another, then one of the Hamiltonian cycles might not form a loop.
Contributed by: Lajos Szilassi (May 2012)
With additional contributions by: János Karsai and Sándor Kabai
Open content licensed under CC BY-NC-SA
Snapshots
Details
In 1861, A. F. Möbius showed that a complete graph with seven vertices can be drawn on the surface of a torus. Any two vertices of this graph are connected by a single edge and no edges intersect.
In 1949, Á. Császár, in response to a problem presented for a mathematical competition for secondary school students, constructed a polyhedron having no intersecting faces, whose combinatorial structure is a Möbius torus (Cs0).
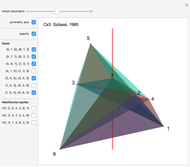
In 1985, L. Szilassi, while producing a less compact version (Cs1) of the polyhedron Cs0, found a "visibly" different version, which can be produced by continuously moving the coordinates of the points, where the faces of the polyhedron get intersected by one another (Cs3).
In 1986, J. Bokowski proved that the Császár polyhedron has four visibly different versions with the same combinatorial structure. He also confirmed that no other versions exists. Cs2 and Cs4 were constructions by Bokowski.
For more information, visit any of the following links:
http://www.mi.sanu.ac.rs/vismath/visbook/csaszar/index.html
http://upcommons.upc.edu/revistes/bitstream/2099/1038/1/st13-06-a3-ocr.pdf
http://upcommons.upc.edu/revistes/bitstream/2099/1067/1/st17-10-a7-ocr.pdf
http://www.eg-models.de/models/Classical_Models/2001.02.069/_direct_link.html
Permanent Citation
"Morphing the Császár Polyhedron"
http://demonstrations.wolfram.com/MorphingTheCsaszarPolyhedron/
Wolfram Demonstrations Project
Published: May 29 2012