Morse-Smale Flows on a Tilted Torus

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
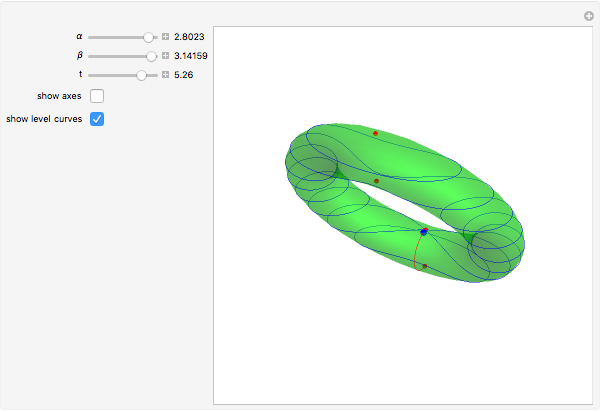
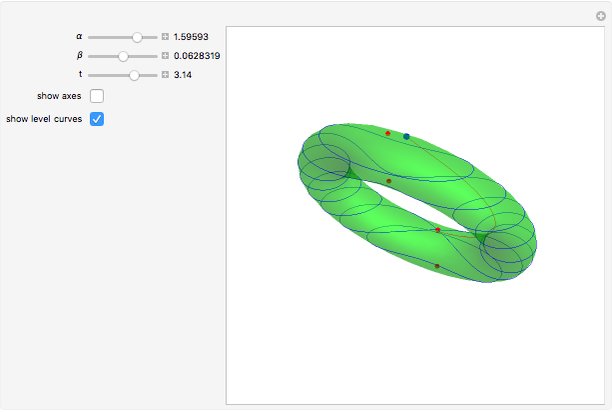
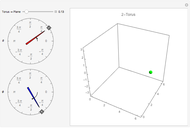
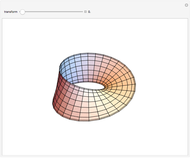
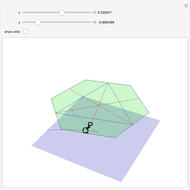
This Demonstration shows the gradient flows of the height function on a tilted torus. It illustrates the basic concepts of Morse theory: the critical points of a Morse–Smale function and their stable and unstable manifolds. The position of a point on the tilted torus is determined by two parametrization angles 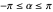 and
and 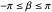 , which define a local coordinate system at each point of the torus. The parameter
, which define a local coordinate system at each point of the torus. The parameter  (which can be negative) controls the duration of the flow.
(which can be negative) controls the duration of the flow.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Morse theory is a generalization of the calculus of variations that relates the stationary points of a smooth real-valued function on a manifold to the global topology of the manifold. A Morse function is a smooth function 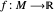 such that all its critical points are nondegenerate and all the critical values are distinct. Each critical point of a Morse function has an index: the number of negative eigenvalues of its Hessian (computed in a local coordinate system in a neighborhood of the point). The indices of all the critical points are closely related to the global topology of the manifold.
such that all its critical points are nondegenerate and all the critical values are distinct. Each critical point of a Morse function has an index: the number of negative eigenvalues of its Hessian (computed in a local coordinate system in a neighborhood of the point). The indices of all the critical points are closely related to the global topology of the manifold.
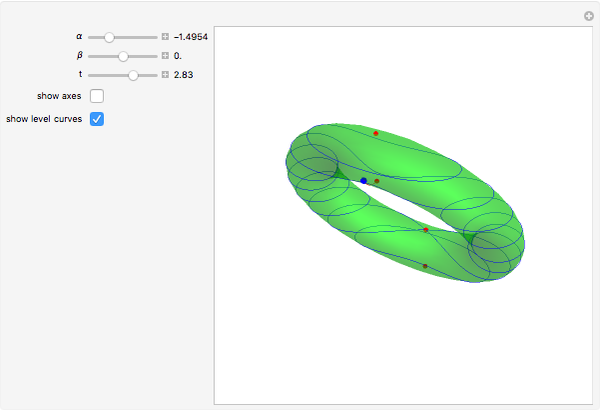
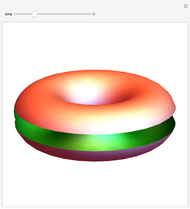
The example of a vertical torus with the height above the ground level as the Morse function first appeared in the classical text [1], which introduced the subject of Morse theory on finite-dimensional manifolds to geometers and topologists. In later work on the subject, due to Floer and Witten, the gradient flow lines of a Morse function play the central role. For each critical point 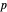 , the set of all regular points whose flow lines end at
, the set of all regular points whose flow lines end at 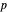 is the stable manifold of
is the stable manifold of 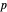 , the set of all regular points whose flow lines originate at
, the set of all regular points whose flow lines originate at 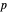 is the unstable manifold of
is the unstable manifold of 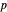 . In order to relate the flow lines to the topology of the manifold it is necessary to ensure that the stable and unstable manifolds of any two critical points intersect transversally (a Morse function with this property is called a Morse–Smale function). In the case of the torus and the height function, this is achieved by tilting the torus slightly.
. In order to relate the flow lines to the topology of the manifold it is necessary to ensure that the stable and unstable manifolds of any two critical points intersect transversally (a Morse function with this property is called a Morse–Smale function). In the case of the torus and the height function, this is achieved by tilting the torus slightly.
In the Demonstration you can choose any regular point on the torus and make the time flow forward or backward to determine which stable or unstable manifolds the point belongs to.
[1] J. Milnor, Morse Theory, Annals of Math. Studies 51, Princeton: Princeton Univ. Press, 1963.
[2] H. Edelsbrunner and J. L. Harer, Computational Topology, An Introduction, Providence, RI: AMS, 2010.
Permanent Citation